Zbiór wartości funkcji Max:

	−π		π
Znajdź zbiór wartości α∊<		;		> dla których równanie (2sinα−1)x2−2x+sinα=0 ma dwa
	2		2

różne pierwiastki rzeczywiste. Proszę o pomoc.

Max: Odświeżam.

Max: Podbijam, proszę o pomoc.

Mila: (2sinα−1)x²−2x+sinα=0

	1
1) 2sinα−1=0 ⇔sinα=		wtedy mamy równanie:
	2

	1
−2x+		=0 jest tylko jedno rozw.
	2

	1
sinα≠		mamy równanie kwadratowe>
	2

2) Δ=4−4*sinα*(2sinα−1)=4−8sin²α+4sinα Δ>0⇔ −8sin²α+4sinα+4>0 sinα=t, |t|≤1 −8t²+4t+4>0 Δ_t=16+4*4*8=144

	−4−12		−4+12
t=		lub t=
	−16		−16

	1
t=1 lub t=−
	2

	1		1
t∊(−		,1) i t≠
	2		2

	1		1		1
−		<sinα<		∪		<sinα<1
	2		2		2

Rozwiąż teraz te nierówności i wybierz odpowiednie przedziały.

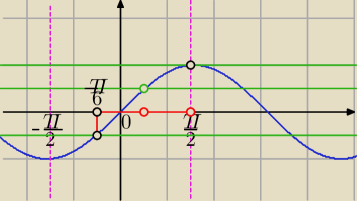
Mila: A właściwie, to odczytaj z wykresu, gdzie masz zaznaczone wszystko co potrzebne.