Liczby zespolone. blabla: Korzystając ze wzoru de Moivre’a obliczyć:

	1		√3
(−		+i		)6
	2		2

Policzyłem: |z|=1

	1		π
cosφ = −		= −sin
	2		6

	√3		π
sinφ = −		= cos
	2		6

	π		π
16(cos6*		+isin		=−1
	6		6

Czy dobrze to policzyłem? czy w miejsce cosφ mam wstawic −sinφ i w sinφ wstawic cosφ? P.S.

	π		2
Czy wartości π dla cos i sin moga być różne? Np.: dla cos		a dla sin		π?
	6		3

Mila:

	1
cosφ=−
	2

	√3
sinφ=		kąt II ćwiartki
	2

	π		2π
φ=π−		=
	3		3

z⁶=|z|*(cos(6φ)+i sin(6φ))⇔

	2π		2π
z6=(cos(6*		)+i sin (6*		))=
	3		3

=cos(4π+i sin (4π))=cos(0)+i sin (0)=1

blabla: @Mila:

	π
Możesz mi powiedzieć dlaczego akurat odejmowałaś od π, a nie np. od		?
	2

Jeśli możesz proszę o odpowiedz na moje wcześniejsze pytanie.

blabla: To mógłby mi to ktoś wyjaśnić?

Mila:

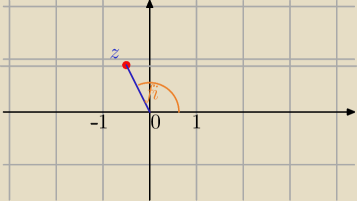
	1		√3
z=(−		,		)
	2		2

	1
cosx=
	2

	π		π
x=		+2kπ lub x=−		+2kπ masz serię rozwiązań
	3		3

Dla równania :

	1
cosx=−		masz serię rozwiązań:
	2

	π		π
x=		+π+2kπ lub x=−		+π+2kπ
	3		3

Kąt ma być II ćwiartki, bo sinx ma być dodatni .

	2π
Wybierasz kąt: φ=
	3

Kąt φ ma być taki sam dla obu funkcji we wzorze de Moivre'a.

blabla: Super Bardzo dziękuje za pomoc Mila

Mila: