M ma dwa rozwiazania ujemne Jack: wyznacz wartości parametru m dla których równanie ma dwa rozwiązania ujemne

Mila: I gdzie to równanie?

Jack: powiedzmy, że mam taką funkcje.

Jack: albo nie , bo z tego to nie wyjdzie, no to mam np. 2|x+1| −3 = m Mam to rozwiazac w sposob graficzny. Najpierw rysujac f(x) = 2|x+1| − 3 a potem odczytujac z wykresu ...

Jack: a więc?

Metis: 2|x+1|−3=m 2|x+1|=m+3 /:2

	m+3
|x+1|=
	2

Rysuj |x+1|, potem "ciachaj" prostą y=m

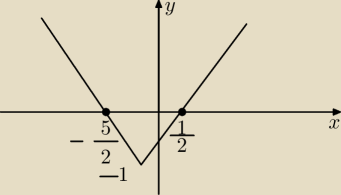
Jack: f(x) = 2|x+1| − 3

Jack: no wlasnie, nie wiem o co chodzi z tym ciachaniem

Jack: hmm]

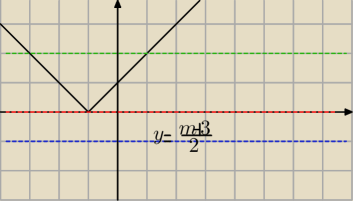
Metis: Masz zadanie: Określić liczbę rozwiązań w zależności od parametru m. 2|x+1| −3 = m Przekształcamy i otrzymujemy:

	m+3
|x+1|=
	2

f(x)=|x+1| Rysujesz wykres, który nie wyglada tak jak ten twój.

Jack: wiec dwa rozwiazania ujemne ma dla...?

Jack: Dlaczego rysuje prosta y = 2?

Metis: I teraz patrzymy na wykres i naszą prostą. Jeśli y=0 jedno rozwiązanie Jeśli y>0 dwa rozwiązania Jeśli y<0 brak rozwiązań

	m+3
y=0 ⇔		=0
	2

	m+3
y>1 ⇔		>1
	2

	m+3
y<1 ⇔		<1 − rozwiąz.
	2

Metis: Narysowałem przykładowo akurat y=2.

Metis:

	m+3
Oczywiście y<0 ⇔		<0
	2

	m+3
y>0 ⇔		>0
	2

Jack: No dobra, powiedzmy...ale z wykresu odczytaj to chyba ≠ rozwiaz rownaniami

Metis: To sposób graficzny, nie algebraiczny. W obu przypadkach wyjdzie przecież to samo.

Jack: A jak mam takie coś? : y = 3^|x+2|

Metis: No i co z tą funkcją?

Jack: to samo polecenie...

Metis: Nie widzę tu zadnego parametru m. Napisałeś po prostu wzór funkcji.

Jack: no tak, narysuj ta funkcje i odczytaj rozwiazania 3^|x+2| = m

Jack: Metis, nie masz moze gg, albo czegos takiego?

Metis: Mam , ale chwilowo nie mam czasu, trzaskam analizę. 3^|x+2|=m f(x)=3^|x+2| Rysujemy f(x) oraz prostą y=m http://i.imgur.com/iwQV6l2.png 1) y=1 ⇔ m=1 − jedno rozwiązanie 2) y<1 ⇔ m<1 − brak rozwiązań 3) y>1 ⇔ m>1 − dwa rozwiązania

Jack: dlaczego akurat prosta 3? rysujesz tak po prostu bye jaka? co do tego gg, szkoda, bo mi zalezy bardzo ; D

Jack: skoro chce dwa rozwiazania ujemne... wiem ze dwa rozwiazania sa dla y>1

Metis: Tak, normalnie tą prostą "jeździsz" po wykresie i odczytujesz.

Jack: ale skad mam wiedziec kiedy sa ujemne, skoro calosc jest na osia X

Metis: Ale co ujemne ? Badasz liczbe rozw. w zaleznosci od m

ZKS: Można popróbować w ten sposób. 3^{|x + 2|} = m Założenie m > 0, dla m ≤ 0 mamy brak rozwiązań log₃(m) = |x + 2| Dla log₃(m) < 0 mamy brak rozwiązań dla log₃(m) = 0 mamy jedno rozwiązanie dla log₃(m) > 0 mamy dwa rozwiązania.

Jack: no tak, ale jesli chce zbadac kiedy sa 2 rozwiazania ujemne... no to dwa rozwiazania w ogole sa dla y>1 i teraz jak odczytac...

Jack: Naprawde nikt nie chce pogadac na gg... 37209167

Jack: Dobra, chyba juz wszystko jasne

ZKS: Dwa ujemne mamy, kiedy |x + 2| = log₃(m) x = log₃(m) − 2 < 0 ∧ x = −log₃(m) − 2 < 0 log₃(m) < 2 ∧ log₃(m) > −2

	1		1
m < 9 ∧ m >		⇒ m ∊ (		; 9) należy jeszcze pamiętać, że dwa rozwiązania mamy dla
	9		9

m > 1, więc m ∊ (1 ; 9).

Jack: Dzięki wielkie.