. NG: Oblicz tangens kąta ostrego jaki tworzą styczne do okręgu o: x²+y²−8x−6y+21=0 przechodzące przez pkt P(2,−1) Obliczyłam S(4,3) i r=2 l: y−ax+b po podstwieniu pkt P y=ax−2a−1 →ax−y−2a−1=0 z d(S,l) otrzymałam równanie prostej l , jednak nie wiem co dalej

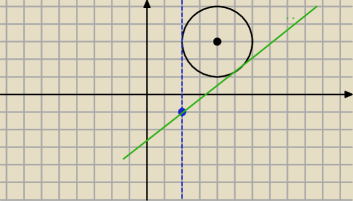
5-latek: Zrobilem rysunek według Twoich obliczen Widzisz z tego z ejedna styczna ma równanie x=2 Druga styczna ma równanie y=m(x−2)+1 wiec y−mx+2m−1=0 to mx−y−2m+1=0 wiemy ze d=2 wiec ze wzoru na podleglosc punktu S=(4,3) od prostej wyznacz m

	|mx0−y0−2m+1|
d=
	√m2+1

Podstaw dane i wylicz m

Mila: x²+y²−8x−6y+21=0 ⇔ (x−4)²−16+(y−3)²−9+21=0 (x−4)²+(y−3)²=4 y=ax+b x=2 jedna styczna −1=2a+b⇔b=−1−2a k: y=ax−1−2a k: ax−y−1−2a=0

	|4a−3−1−2a|
d(k,S=(4,3))=2=
	√a2+1

|2a−4|=2*√a²+1 /² 4a²−16a+16=4a²+4 16a=12

	3
a=
	4

	3		3
k: y=		x−1−
	4		2

	3		5
k: y=		x−
	4		2

	3
tgα=
	4

Dalej spróbuj sama Będę za godzinę.

NG: A to nie powinno mi wyniknąć z obliczeń a nie z rysunku?

5-latek: Dobry wieczor Milu Pozdrawiam

NG: Dziękuję! Wszystko przez to, że nie zrobiłam rysunku i nie ogarnęłam, że jedną styczną jest x=2.

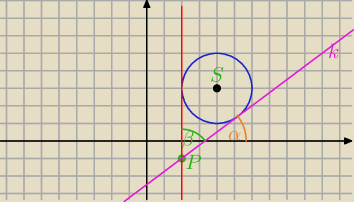
	|A1B2−B1A2|
tgβ wyliczyłam już ze wzoru
	|A1A2+B1B2|

5-latek: Rysunek jest tak samo pełnoprawnym rozwiązaniem tak samo jak obliczenia Jeśli chcesz wykonać obliczenia to zauważ ze pek prostych przechodzących przez punkt P ma rownie y=m(x−x₀)+b czyli y=m(x−2)−1 Tam poprzednio napisałem zle (teraz zauwazylem błąd Bo jest y−y₀=m(x−x₀) to y=m(x−x₀)+y₀ wiec jak posdtawimy wspolrzedne punktu P mamy y−(−1)=m(x−2) to y+1=m(x−2) to y=m(x−2)−1 ============== Rownanie okręgu jest takie x²+y²−8x−6y−21=0 Podstaw y to tego równania i policz m

5-latek: Jeśli jesteś studentka to powinnas wiedzieć ze tg kata pomiędzy prosta x=a i prosta y=mx+b można wyznaczyć ze wzoru

	1
tgφ= ±
	m

NG: Nie jestem studentką , maturzystką