postać ogólna funkcji
ewret: Wiadomo że funkcja kwadratowa przyjmuję najmniejszą wartosć równą −1 oraz że f(−4)=f(2)=2.
Przedstaw tę funkję w postaci ogólnej.
2 gru 23:06
cos tam:
skoro przyjmuje najmniejsza wartosc to jak wyglada parabola ?
skoro dla dwoch argumentow przyjmuje ta sama wartosc to co ?
2 gru 23:09
ewret: parabola w dól?
2 gru 23:09
cos tam:
czy jesli ramiona paraboli skierowane sa w dol to mozna powiedziec jaka jest najmniejsza
wartosc ? (pomysl
)
2 gru 23:11
ewret: kiepska jestem
−1 jest najmniejszą wartości
pomóż proszę
2 gru 23:12
ewret: jak przedstawić funkcje w postaci ogólnej?
2 gru 23:12
Janek191:
q = − 1
f(−4) = 2 i f(2) = 2
więc
f(x) = a*( x − p)
2 + q = a*( x + 1)
2 − 1
oraz
| | 1 | |
f(−4) = a*( − 4 + 1)2 − 1 = 9 a − 1 = 2 ⇒ 9 a = 3 ⇒ a = |
| |
| | 3 | |
dlatego
| | 1 | |
f(x) = |
| *( x + 1)2 − 1 − postać kanoniczna |
| | 3 | |
| | 1 | | 1 | | 2 | | 2 | |
f(x) = |
| *( x2 + 2 x + 1) − 1 = |
| x2 + |
| x − |
| |
| | 3 | | 3 | | 3 | | 3 | |
2 gru 23:15
cos tam:
otoz ramiona skierowane sa w gore, wtedy mozemy powiedziec o najmniejszej wartosci.
jesli dla dwoch argumentow wartosc funkcji kwadratowej jest taka sama to 'po srodku' tychze
argumentow znajduje sie wierzcholek. Korzystajac z tych informacji rozwiaz zadanie
2 gru 23:15
cos tam:
no i poszlooo
2 gru 23:16
Janek191:
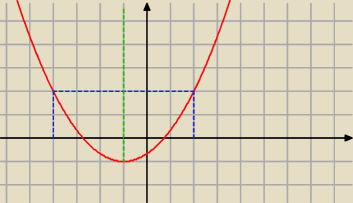
2 gru 23:16
ewret: dziękuje
2 gru 23:22
Janek191:
Wiesz, która postać jest ogólna ?
2 gru 23:25