dziedzina
ktry: wyznacz dziedzine √x2−3x+2+1/√3+2x−x2
2 gru 22:02
Jack: pierwszy pierwiastek :
≥ 0
drugi skoro jest mianownikiem , to tylko >0
2 gru 22:03
ktry: w pierwszym delta, tak ?
2 gru 22:04
ktry: x=(−3,1)v<2,+nieskon)

2 gru 22:07
Jack: no mialem na mysli że :
x2−3x+2 ≥ 0
oraz
3+2x−x2 >0
w obydwóch liczych delte
miejsca zerowe
zaznaczasz na osi
znajdujesz przedzial...
2 gru 22:08
ktry: no wyszło mi coś, możesz zobaczyć czy dobrze ?

2 gru 22:09
Jack: skąd taki przedział? ; o
2 gru 22:10
Jack:
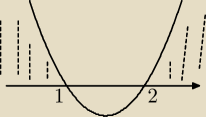
2 gru 22:11
dominika: XD
2 gru 22:11
Jack: Czy juz podajesz koncowy?
2 gru 22:11
ktry: x2−3x+2 ≥ 0
x1=1, x2=2
3+2x−x2 >0
x1=−3, x2=1
2 gru 22:12
Jack: Ta druga oblicz jeszcze raz

2 gru 22:13
ktry: no tak, w pierwszym tak mi wyszło
tylko cos w tym drugim namieszałem
2 gru 22:14
ktry: x1=3, x2=−1

2 gru 22:15
Jack: tak jest, czyli :
2 gru 22:15
Jack: Część wspólna obu

2 gru 22:16
ktry: ramiona skierowane do dołu czyli x=(−1,3)
2 gru 22:16
Jack: nom...
czyli pierwszy : x∊(−∞;1> U <2;∞)
drugi : x∊(−1;3)
Część wspólna :
2 gru 22:18
ktry: x=(−1,1)v(2,3)
2 gru 22:18
Jack: (−1;1 > U <2;3)
pamiętaj o domknięciach
2 gru 22:20
ktry: dzięki wielkie

2 gru 22:20
Jack: Nmzc

2 gru 22:22
ktry: to może jeszcze w jednym mi pomozesz ?

2 gru 22:25
ktry: log2 (x2−5x)
2 gru 22:25
ktry: log czyli >0
2 gru 22:26
Jack: Nadal potrzebne , czy ?

3 gru 21:01









