f,logarytmiczna krotki: Wie ktos jan to zrobić ? W wyniku przekształcenia wykresu funkcji f(x)=log₂ x przez symetrię względem prostej y=x otrzymam wykres,funkcji... I odp,to y=2^x skąd to się bierze !?

krotki:

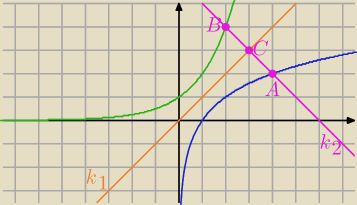
Bogdan: A(x_A, y_A), k₁: y = x k₂⊥k₁ ⇒ k₂: y = −(x − x_A) + y_A ⇒ y = −x + x_A + y_A

	1		1
C = k1∩k2 ⇒ x = −x + xA + yA ⇒ x =		xA +		yA i y = x
	2		2

	1		1		1		1
C = (xC, yC) = (		xA +		yA,		xA +		yA)
	2		2		2		2

B = (x_B, y_B), x_B = 2x_C−x_A = x_A+y_A−x_A = y_A, y_B = 2y_C−y_A = x_A+y_A−y_A = x_A B = (y_A, x_A) Obrazem każdego punktu (x, y) wykresu y = log₂ x w symetrii osiowej względem prostej y = x jest punkt (y, x), czyli obrazem punktu (x, y = log₂x) jest punkt (y, x = log₂y) x = log₂y ⇒ y = 2^x