geometria Aga: Podstawą graniastosłupa prostego jest romb o boku długości 8 i kącie ostrym a=60^o. Wiedząc że dłuższa przekątna graniastosłupa d=20, oblicz długość jego krótszej przekątnej, pole powierzchni całkowitej i objętość.

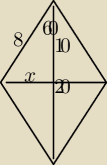
Aga: Czy x powinnam obliczyć Pitagorasem? x² + 10² = 8² x²= 64−100 x²= − 36 :l

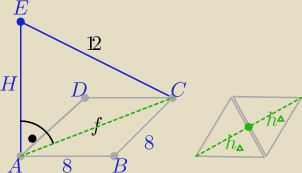
Eta: Ten romb składa się z dwu trójkątów równobocznych o boku dł. a=8

	a√3
to f= 2*		= 8√3
	2

P_p=P(ABCD)= 8*8*sin60^o= 32√3 Z trójkąta prostokątnego ACE : H= √12²−f²= ..... V= P_p*H=.... P_C= 2P_p+ 4a*H=.... dokończ obliczenia

sam: Graniastosłup czworokątny ma tylko 1 przekątną

Eta: @ sam Czytanie ze zrozumieniem się kłania w treści napisano : " dłuższa przekątna graniastosłupa ma długość 12" zatem jest nią długość odcinka |EC|=12

sam: No tak to jest dłuższa przekątna, ale w żadnej książce, nie jest napisane, że wysokość, czy krawędź ściany bocznej jest również przekątną... Zadanie jest rozwiązane dobrze, ale polecenie jest bez sensu sformułowane i nie każdy może wiedzieć o co chodzi.

Aga: długość odcinka |EC|=20 H= √ 20² − (8 √3)² = √400−192 = √208 V= 32 √3 * √208 Pc= 64 √3 + 32 {208} tak to ma wyglądać? undefined

Aga: Może ktoś sprawdzić?

Eta: No tak ,źle wpisałam |EC|=20 ( a nie 12 H= √208=√16*13= 4√13 V=.... P_C=....

Eta: Jest ok wpisz tylko zamiast √208 = 4√13

Aga: dziękuję Ci bardzo

Eta: Na zdrowie ....