największa/najmniejsza wartość funkcji Metis: Oblicz największą i najmniejszą wartość funkcji danej wzorem f(x) = |x²−8x+7| w przedziale [0,5]. Jak obliczyć wartość najmniejszą? f(x) = |x²−8x+7| ▯x²−8x+7, jeśli x∊(−∞, 1] U [7, +∞) f(x)= ▯−x²+8x−7, jeśli x∊ (1,7) Liczę f(0) ∧ f(5) oraz x_w f(0)=7 f(5)=8 x_w=4 x_w∊[0,5] Stąd y_w=9 Wartość największa y_max=9 Nie wiem co z wartością najmniejszą. Z wykresu widać że f(1)=0 , y_min=0

52: Hmmm... jeśli nie chcesz korzystać z wykresu to wiesz że jeśli masz funkcje kwadratową i ma ona miejsca zerowe a potem nałożysz na nią wartość bezwzględną to najmniejsza wartość takiej funkcji to 0 Zatem przyrównać f(x) do 0 i modlić się aby w zadanym przedziale wyszło rozwiązanie Ale nie wiem czy to cię zadowoli

Metis: No to jasne Dzięki 52 Tylko jak to wszystko ładnie zapisać, by zapis był poprawny. Bo w takim przypadku okazuje się, że liczenie f(0) i f(5) jest zbędne. Może tego rodzaju funkcję badać z pomocą analizy matematycznej ?

52: Kurcze, rozbijać na pochodne patrzeć przedziały, trochę z tym roboty by było... Tak na prawdę to moim skromnym zdanie to wykres najlepiej wszystko oddaje

Metis: Moim też ale jednak wolę piękny, przejrzysty zapis algebraiczny . Poczekam na wybitne jednostki. Może PW skusi się na piękne rozwiązanie

Godzio: f(x) ≥ 0 więc najmniejsza wartość jest przyjmowana dla argumentu, dla którego f(x) = 0, Sprawdzamy czy miejsca zerowe zawierają się w przedziale. x² − 8x + 7 = (x − 7)(x − 1) x = 1 ∊ [0,5] Stąd 0 jest najmniejszą wartością. Policzmy największą:

	8
p =		= 4 ∊ [0,5]
	2

f(4) = 9 f(0) = 7 f(5) = 8 Max: 9, Min: 9

Godzio: Min: 0 oczywiście

Metis: O, Dzięki Wielkie Godzio

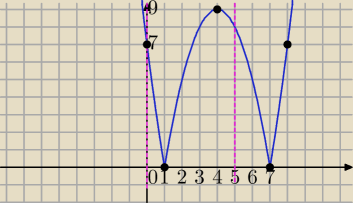
Mila: f(x) = |x²−8x+7| g(x)=x²−8x+7 Δ=64−28=36 x₁=1 lub x₂=7 x_w=4, y_w=16−32+7=−9 |y_w|=9 szkicuję wykres f(x) f(1)=0=f_min f(4)=9=f_max

Metis: Dziękuje Milu

Mila: Gratuluję ładnego wyniku na próbnej, uzupełniaj braki, aby w maju było 100%. Jak napisała Twoja klasa?

Saizou : Można też skorzystać z twierdzenia Weierstrassa o osiąganiu kresów przez funkcję ciągła. W tym przypadku mamy funkcje g=|f| jest ona ciągła i przyjmuje wartości nieujemne, zatem g min jest w punktach gdzie g się zeruje a g max jest dla największej liczby z przedziału [0,5]

Metis: Dziękuje serdecznie Milu . Niestety ja jestem paradoksem, i nawet jeśli będę umiał dużo, to zawsze gdzieś coś skopię, źle na mnie wpływa stres Moja klasa napisała słabo, wyniki 30%, 40%, a nawet 3% i 6% . Ale, niektórzy poszli na rozszerzenie "od tak", rozmyślają czy zdawać R z matematyki, mimo że wszyscy chodzimy do klasy o nachyleniu matematycznym Niestety wyniki mojej klasy zawsze są ponizej sredniej innych klas i całej szkoły. Ostatnia klasa, ta "budżetowa" Ja na początku zmieniłem klasę, w pierwotnej było 37 osób, straszny tłok. W miarę roku postępu roku szkolnego żałowałem swojej decyzji.

Mila: Teraz sam musisz dużo pracować, na pewno będzie dobrze.