Zadanie z ostrosłupów
Newbie: Czy jest ktoś kto czuje się dobry w zadaniach z ostrosłupami?
Gdyż mam kilka zadań po kolejnej już poprawie i nie mam pojęcia jak poprawnie je rozwiązać

1 gru 19:19
Jack: nigdy tego nie ogarnialem wiec wklejaj

1 gru 19:20
Newbie: 1)Krawędź boczna ostrosłupa prawidłowego czworokątnego o krawędzi podstawy długości 4 jest
nachylona do płaszczyzny podstawy pod kątem 30°.
Oblicz objętość tego ostrosłupa.
2)W ostrosłupie prawidłowym sześciokątnym miara kąta między wysokością ostrosłupa i wysokością
ściany bocznej jest równa 30°. Długość wysokości tego ostrosłupa jest równa 6. oblicz pole
powierzchni tego ostrosłupa.
3)Podstawa ostrosłupa jest równoramienny trójkąt prostokątny o przeciwprostokątnej długości 4.
Krawędź boczna ostrosłupa poprowadzona z wierzchołka Kąta prostego ma długość 6 i jest
prostopadła do płaszczyzny podstawy, oblicz sumę długości wszystkich krawędzi tego
ostrosłupa.
1 gru 19:23
Newbie: Później miałem zadanie takie:
Oblicz pole powierzchni całkowitej czworościanu foremnego o krawędzi długości 10 cm.
Odp. Czy dobrze myślę, że jeśli to 4 trójkąty równoboczne to jeśli pole jednego wynosi 25√3
to całość ma 100√3 ?
1 gru 19:25
5-latek: Dobrze myślisz
1 gru 19:27
Jack: P
c = a
2 √3 = 100
√3 cm
2
dokladnie

1 gru 19:27
Newbie: JEA

A czy uzyskam pomoc co do tych 3 trudnych dla mnie zadań ?
1 gru 19:29
Jack:
1 gru 19:32
Newbie:
30
1 gru 19:34
Newbie: o ile Pp to 4x4 bo to kwadrat to brakuje mi wysokości ostrosłupa, a mam podany tylko kąt
1 gru 19:35
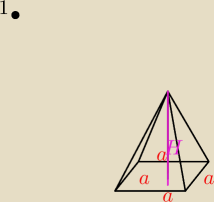
Jack: 1.
skoro podstawa to kwadrat
to X jest polowa przekatnej czyli
4
√2 / 2 = 2
√2
| | 1 | |
V = |
| * 4 * 4 * 2√2 * tg 30 |
| | 3 | |
| | 1 | | √3 | |
V = |
| * 16 * 2√2 * |
| |
| | 3 | | 3 | |
1 gru 19:40
Newbie: Jacek kurde teraz to widzę!
1 gru 19:43
Jack:
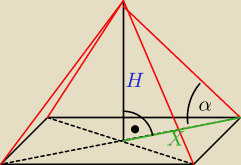
Takie oznaczenia przyjalem w pierwszym zadaniu
1 gru 19:44
Jack:
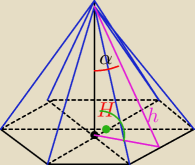
H = 6
1 gru 19:51
Newbie: Dokładnie tak to sobie rozrysowałem.
I teraz x może być wysokością trójkąta równobocznego w podstawie czyli a3/2
1 gru 19:58
Newbie: oczywiście 2√3/2
1 gru 19:58
Newbie: ale co dalej

1 gru 19:59
Jack: zad 2.
H = 6
α = 30
P
c = P
p + P
b
| | a2√3 | | 3a2√3 | |
Pp = 6 * PΔrownobocznego = 6 * |
| = |
| |
| | 4 | | 2 | |
P
b = 6 * P
Δ = 6 * (a*h/2) = 3 * a * h
| | 2H | | 12 | | 12√3 | |
h = |
| = |
| = |
| = 4√3 |
| | √3 | | √3 | | 3 | |
| | √3 | |
x = h * tg 30 = 4√3 * |
| = 4 |
| | 3 | |
a więc
x to w tym wypadku wysokosc jednego z trojkatow rownobocznych w podstawie, czyli
| | a√3 | | 2x | | 8√3 | |
x = |
| , więc a = |
| = |
| |
| | 2 | | √3 | | 3 | |
Podstawiając wszystko :
P
b = 3 * a * h = 96
P
c = 96 + 32
√3 = 32 (3+
√3)
1 gru 20:09
Jack: Wszystko jasne?

1 gru 20:15
Newbie: I Ty tego nie ogarniasz

1 gru 20:24
Newbie: Jasne właśnie przeszedłem krok po kroku i widzę, że kurde niby nic skomplikowanego, ale na
pierwszy rzut oka nie widać tego

DZIEKUJĘ
1 gru 20:24
Newbie:
1 gru 20:31
Jack: jasne ze nie ogarniam. Nie mialem jeszcze takich rzeczy. W planimetrii tego nie ma

. Dlatego
musze sprawdzac jak wyglada kazda figura ktorej dotyczy zadanie...
dobra to teraz zad 3
1 gru 20:31
Newbie:
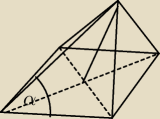
Na rysunku dany jest ostrosłup prawidłowy czworokątny,
w którym wysokość jest dwa razy krótsza niż krawędź podstawy. Oblicz miarę kąta a.
1 gru 20:36
Jack:
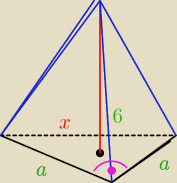
1 gru 20:39
Jack: To co wkleilas, bez zadnych danych to wzor wyznaczyc?
1 gru 20:44
Newbie: Był taki rysunek i obliczyć kąt α należy.
1 gru 20:54
Jack:
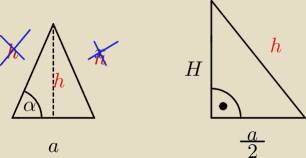
Twoje zadanie :
Rozpatrujemy dwa trójkąty
Oznaczenia jak na rysunkach.
Z pierwszego wyznaczamy tangens
z drugiego :
Z polecenia :
a = 2H
1 gru 20:59
Jack: poprawka.
Z pierwszego
czyli
wiemy, że a = 2H
czyli do pitagorasa :
h
2 = H
2 + (H)
2
h
2 = 2 H
2
h = H
√2 lub h = −H
√2 (ale jakikolwiek bok ani wysokosc nie moze byc ujemna).
Dlatego mamy :
| | 1 | |
h = H√2 oraz wiemy , że h = |
| a * tg α, czyli : |
| | 2 | |
2H
√2 = a*tg α
Z polecenia że a = 2H :
czyli tg α =
√2
α = ...
1 gru 21:05
Newbie: Ale jak obliczyć tą miarę kąta α ?
1 gru 21:09
Newbie: A spoko z tablicy.. oki
1 gru 21:10
Jack: raczej z tablicy ale nie jestem pewien

1 gru 21:12
Newbie: Tego nie ogarniam
h2 = H2 + (H)2
h2 = 2 H2
1 gru 21:13
Jack: No mamy, że
z polecenia
a = 2H
więc
czyli
H
2 + H
2 = h
2
1 gru 21:16
Newbie: a dlaczego a/2 ?
1 gru 21:19
Jack: bo (drugi rysunek trojkata) = pitagoras
1 gru 21:20
Newbie: Myślę, że to połowa przekątnej kwadratu w podstawie? Czyli a√2/2
1 gru 21:20
Newbie: I dlaczego długość krawędzi bocznej ma taką samą długość jak wysokość trójkąta ?
1 gru 21:22
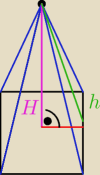
Jack:
1 gru 21:23
Jack: jak widac to jest po prostu polowa podstawy
1 gru 21:23
Newbie: aha w ten sposób, ja myślałem, że po przekątnej po prostu
1 gru 21:24
Jack: Coś jeszcze trzeba by było wyjaśnić? bo za 15min zmykam

1 gru 21:28
Newbie: Myślę, że muszę to przeanalizować, a jakbyś jutro mógł zerknąć czy nie napisałem jeszcze
jakiegoś zapytania

Da radę jutro popatrzeć?
1 gru 21:29
Jack: Luzik

a te zadanie 3?
zrobic czy ?
1 gru 21:30
Newbie: chętnie zapoznam się z metodą jego rozwiązywania.
1 gru 21:30
Jack: No to wracając do postu 20:39.
Skoro podstawa to trojkat rownoramiennyi na dodatek prostokatny, a przeciwprostokatna wynosi 4.
Pitagoras :
a
2 + a
2 = 4
2
2a
2 = 16
a
2 = 6
a=2
√2 (odrazu odrzucam ujemna wartosc bo bok nie moze byc ujemny).
Hah, akurat widze, ze na tym rysunku zle oznaczylem te przeciwprostokatna

1 gru 21:39
Jack:
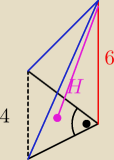
Przepraszam znowu za błąd...
2a
2 = 16
a
2 = 8
i dlatego a=2
√2 
1 gru 21:46
Jack: wiemy więc że
Krawędzie podstawy :
2√2 + 2√2 + 4 = 4 + 4√2 = 4 (1+√2)
Wiemy, że krawędź boczna przy kącie prostym ma długość 6.
Najdłuższą krawędź boczną można obliczyć z Pitagorasa.
(2√2)2 + 62 = c2
c2= 8 + 36
c= √44 = √4*11 = 2√11
Przynajmniej tak mi sie zdaje ze tam jest kat prosty, no bo jest prostopadly do plaszczyzny.
1 gru 21:54
Jack: Ta druga krawedz chyba tez tyle wynosi...
skoro trojkat rownoramienny, to chyba tak

czyli
Krawedzie boczne = 6 + 2
√11 + 2
√11 = 4
√11 + 6
Krawedzie podstawy = 4+4
√2
Czyli wszystkie krawedzie :
4
√11 + 6 + 4 + 4
√2 = 10 + 4(
√2+
√11)
1 gru 21:57
Jack: Nie gwarantuje, ale powiedzialbym ze tak bedzie...Nie masz moze do tego odp. ?

1 gru 21:57
Newbie: Kurcze no właśnie nie mam i to jest problem..
2 gru 16:25
Newbie: A w tym drugim zadaniu tg30 = x/H chyba, a nie x/h ?
2 gru 16:29
Jack: tak, faktycznie

, ale skopalem
3 gru 21:12



 A czy uzyskam pomoc co do tych 3 trudnych dla mnie zadań ?
A czy uzyskam pomoc co do tych 3 trudnych dla mnie zadań ?

 30
30
 Takie oznaczenia przyjalem w pierwszym zadaniu
Takie oznaczenia przyjalem w pierwszym zadaniu
 H = 6
H = 6



 DZIEKUJĘ
DZIEKUJĘ
 . Dlatego
musze sprawdzac jak wyglada kazda figura ktorej dotyczy zadanie...
dobra to teraz zad 3
. Dlatego
musze sprawdzac jak wyglada kazda figura ktorej dotyczy zadanie...
dobra to teraz zad 3
 Na rysunku dany jest ostrosłup prawidłowy czworokątny,
w którym wysokość jest dwa razy krótsza niż krawędź podstawy. Oblicz miarę kąta a.
Na rysunku dany jest ostrosłup prawidłowy czworokątny,
w którym wysokość jest dwa razy krótsza niż krawędź podstawy. Oblicz miarę kąta a.

 Twoje zadanie :
Rozpatrujemy dwa trójkąty
Oznaczenia jak na rysunkach.
Z pierwszego wyznaczamy tangens
Twoje zadanie :
Rozpatrujemy dwa trójkąty
Oznaczenia jak na rysunkach.
Z pierwszego wyznaczamy tangens



 Da radę jutro popatrzeć?
Da radę jutro popatrzeć?
 a te zadanie 3?
zrobic czy ?
a te zadanie 3?
zrobic czy ?

 Przepraszam znowu za błąd...
2a2 = 16
a2 = 8
i dlatego a=2√2
Przepraszam znowu za błąd...
2a2 = 16
a2 = 8
i dlatego a=2√2 
 czyli
Krawedzie boczne = 6 + 2√11 + 2√11 = 4√11 + 6
Krawedzie podstawy = 4+4√2
Czyli wszystkie krawedzie :
4√11 + 6 + 4 + 4√2 = 10 + 4(√2+√11)
czyli
Krawedzie boczne = 6 + 2√11 + 2√11 = 4√11 + 6
Krawedzie podstawy = 4+4√2
Czyli wszystkie krawedzie :
4√11 + 6 + 4 + 4√2 = 10 + 4(√2+√11)

 , ale skopalem
, ale skopalem