 a) − 4 x2 + 16 x < 0
−4 x*( x − 4) < 0
x1 = 0 x2 = 4 oraz a = − 4 < 0 − ramiona paraboli są skierowane ku dolowi,
więc
x ∊ ( −∞ ; 0 ) ∪ ( 4; +∞ )
==================
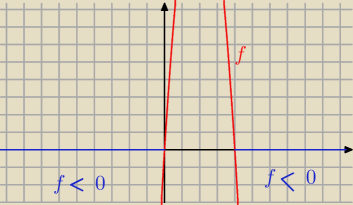
Dodatkowo − wykres f(x) = − 4 x2 + 16
a) − 4 x2 + 16 x < 0
−4 x*( x − 4) < 0
x1 = 0 x2 = 4 oraz a = − 4 < 0 − ramiona paraboli są skierowane ku dolowi,
więc
x ∊ ( −∞ ; 0 ) ∪ ( 4; +∞ )
==================
Dodatkowo − wykres f(x) = − 4 x2 + 16
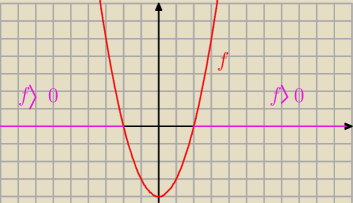 b) 9 x2 − 36 > 0 / : 9
x2 − 4 > 0
( x − 2)*( x + 2) > 0
x1 = − 2 x2 = 2 oraz a = 1 > 0, więc
x ∊ (−∞ ; − 2) ∪ ( 2; +∞)
==================
Dodatkowo − wykres f(x) = x2 − 4
b) 9 x2 − 36 > 0 / : 9
x2 − 4 > 0
( x − 2)*( x + 2) > 0
x1 = − 2 x2 = 2 oraz a = 1 > 0, więc
x ∊ (−∞ ; − 2) ∪ ( 2; +∞)
==================
Dodatkowo − wykres f(x) = x2 − 4
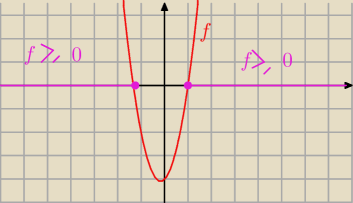 c) 3 x2 + x − 4 ≥ 0
Δ = 12 − 4*3*(−1) = 1 + 12 =13 √Δ = √13
c) 3 x2 + x − 4 ≥ 0
Δ = 12 − 4*3*(−1) = 1 + 12 =13 √Δ = √13
| − 1 − √13 | − 1 + √13 | |||
x1 = | x2 = | |||
| 6 | 6 |
| − 1 − √13 | − 1 +√13 | |||
x ∊ (−∞ ; | > ∪ < | ; +∞ ) | ||
| 6 | 6 |
 Pewnie z sentymentu do swoich stron
Pewnie z sentymentu do swoich stron 