Prawdopodobieństwo Przemysław: Dwie osoby umawiają się, że spotkają się między 12. a 13. Jak któraś z nich przyjdzie, to czeka 20 min i jak druga nie przyjdzie w tym czasie to mówimy, że osoby się nie spotkały. Obliczyć prawdopodobieństwo, że się spotkają. Znam rozwiązanie, ale wolałbym poznać inne, bo tamto − mimo, że je rozumiem tak trochę, to mnie nie przekonuje.

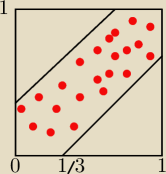
b.: Zdaje się, że jest ono równe polu tej części na czerwono.

Przemysław: No właśnie to znam, ale mnie nie cieszy to rozwiązanie Jakby to powiedzieć... Skąd to się bierze. Jak można odkładać jeden czas na dwóch osiach. Jak to się zgadza z sytuacją.

Przemysław: Mimo wszystko, dziękuję za odpowiedź.

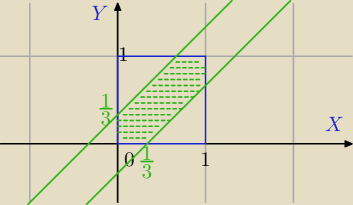
Mila: Dwie osoby mają się spotkać w ciągu godziny. Ω={(x,y): x,y∊<0,1>}

	1
20min=		h
	3

	1
A={(x,y): |x−y|≤		}
	3

	1
|x−y|≤		⇔
	3

	1		1
−		≤x−y≤
	3		3

	1		1
x−y≥−		i x−y≤		⇔
	3		3

	1
y≤x+		obszar pod prostą
	3

i

	1
y≥x−		obszar nad prostą
	3

	μ(A)
P(A)=		⇔
	μ(Ω)

	...
P(A)=		licz pole
	1

PW: Jeżeli czas przybycia jednej z osób oznaczyć symbolem x, x∊(0,1) [jedna godzina między 12:00 a 13:00), a czas drugiej z osób − symbolem y, y∊(0,1), to spotkanie dojdzie do skutku, gdy

	1
(1) |y − x| ≤
	3

	1
(20 minut to		godziny).
	3

Zbiór punktów (x, y), których współrzędne spełniają nierówność (1) tak właśnie wygląda na rysunku w układzie współrzędnych XOY (rozwiązanie nierówności (1) to zbiór punktów (x,y) dla których

	1		1
−		≤ y − x ≤		,
	3		3

czyli

	1		1
x −		≤ y ≤ x +		.
	3		3

Cała przestrzeń Ω to pole kwadratu o boku 1 − każdy z nich może przyjść w dowolnym czasie z przedziału <0, 1>.

Przemysław: Dziękuję bardzo

	5
Ogólnie to		wychodzi?
	9

Mila: PW, Na szczęście 23:46. Ten sam pomysł, Twoje wyjaśnienie jak zwykle przejrzyste. i dobranoc.

PW: Dobranoc