 x − szukana odległość, x > 0
Kluczem do rozwiązania problemu jest znalezienie funkcji którą będziemy maksymalizować.
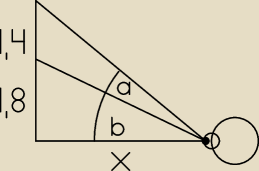
Dla zachowania czytelności mnożę długości boków przez 10. Z rysunku możemy zauważyć że:
x − szukana odległość, x > 0
Kluczem do rozwiązania problemu jest znalezienie funkcji którą będziemy maksymalizować.
Dla zachowania czytelności mnożę długości boków przez 10. Z rysunku możemy zauważyć że:
| 18 | 18 | |||
· tan(β) = | ⇒ β = arctan( | ) | ||
| x | x |
| 14 + 18 | 32 | 32 | ||||
· tan(α + β) = | = | ⇒ α + β = arctan( | ) | |||
| x | x | x |
| 32 | 18 | |||
α = α + β − β = arctan( | ) − arctan( | ) | ||
| x | x |
| a−b | ||
Wykorzystując wzór arctan(a) − arctan(b) = arctan( | ) możemy zapisać, że: | |
| 1+ab |
| 32 | 18 | 14x | ||||
α = α + β − β = arctan( | ) − arctan( | ) = arctan( | ) = d(x) | |||
| x | x | x2+576 |
| d | 14x | −14(x2 − 576) | ||||
arctan( | ) = | |||||
| dx | x2+576 | 196 + (x2+576)2 |
 Punkty stacjonarne są tam, gdzie pochodna funkcji jest równa 0. Funkcja wymierna jest równa 0
wtedy i tylko wtedy gdy jej licznik jest równy 0:
−14(x2 − 576) = 0 ⇒ x = ±24
Przypomnijmy że x jest odległością (x > 0), więc x = −24 należy odrzucić.
Funkcja y = −14(x2 − 576) to parabola, której ramiona skierowane są w dół, więc punkt x = 24
jest jej wierzchołkiem i jednocześnie maksimum tej funkcji.
Punkty stacjonarne są tam, gdzie pochodna funkcji jest równa 0. Funkcja wymierna jest równa 0
wtedy i tylko wtedy gdy jej licznik jest równy 0:
−14(x2 − 576) = 0 ⇒ x = ±24
Przypomnijmy że x jest odległością (x > 0), więc x = −24 należy odrzucić.
Funkcja y = −14(x2 − 576) to parabola, której ramiona skierowane są w dół, więc punkt x = 24
jest jej wierzchołkiem i jednocześnie maksimum tej funkcji.
| 7 | ||
Maksimum to jest równe arctan( | ), czyli ≈ 16,26°. | |
| 24 |