a
kevs: |x2−9|+|x2−16|=m dla jakiego m równanie ma dokładnie 2 różne pierwiastki ?
Otrzymuję 2 przedziały dla x :
1)x∊(−∞;−4u<4;∞) ====> 2x2−7=m
2)x∊<−4;−3)u<3;4) ====>7=m
3)x∊<−3;3) ====>−2x2+25=m
I teraz dla każdego trzeba rozwiązać Δ>0, prawda ? Czyli :
1)Δ=−4(−15−2m)=56+8m
56+8m>0
m>−7
2)brak m
3)Δ=−4(−50+2m)
200−8m>0
m<25
Co robię źle, odpowiedź to m>25
30 lis 21:41
kevs: 
30 lis 21:56
===:
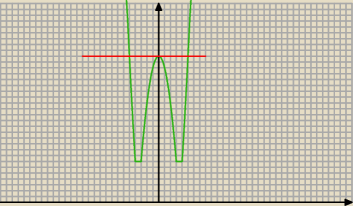
30 lis 22:07
kevs: Ale jak rozwiązać to w sposób algebraiczny ?
30 lis 22:10
===:
nie robić tylu błędów

30 lis 22:12
kevs: Jakich konkretnie ?
30 lis 22:16


