Kolejne zadanie z monotoniczności funkcji i ekstrema
Monika: zbadać monotoniczność funkcji
f(x) =1/e do potęgi x−4
30 lis 14:06
J:
1) Dziedzina
2) Pochodna
30 lis 14:11
Monika: właśnie ja tego nie rozumiem jaka jest dziedzina
30 lis 14:14
J:
| | 1 | |
f(x) = |
| .. czy mianownik może przyjąc wartość 0 ? |
| | ex−4 | |
30 lis 14:22
Monika: ma być różny od 0 , tak ?
30 lis 14:27
J:
tak
30 lis 14:28
Monika: czyli zbior liczb rzeczywistych dziedzina
30 lis 15:19
J:
tak , teraz pochodna
30 lis 15:20
Monika: zaraz wysle odpowiedz tylko sobie w zeszycie rozwiaze
30 lis 15:22
Monika: odpowiedz to pochodna wynosi 4ex/ex−8
Tak ?
30 lis 15:25
Monika: ta ósemka w potędze
30 lis 15:25
Monika: nie wiem byc może jakiś błąd zrobiłam , jesli tak prosze mnie poprawic
30 lis 15:26
J:
| | e4 | |
f(x) = |
| ... i teraz licz pochodną |
| | ex | |
30 lis 15:28
Monika: e4 to pochodna bedzie e ?
30 lis 15:31
J:
pochodna stałej = ?
30 lis 15:32
Monika: pochodna z ex = ex
30 lis 15:33
J:
przecież e4 to stała ( konkretna liczba) i jej pochodna wynosi ?
30 lis 15:34
Monika: nadal nie wiem , wydaje mi sie ze ex
30 lis 15:36
J:
nie , pochodna stałej = 0
30 lis 15:37
Monika: aha rozumiem czyli odpowiedz pochodna wynosi −e4*ex/ex2 tak ?
30 lis 15:42
J:
skróć przez: ex
30 lis 15:44
Monika: czyli −e4/ex , tak ?
30 lis 15:47
Monika: w mianowniku ex
30 lis 15:47
J:
tak ... teraz ustal jaki ma znak ta pochodna
30 lis 15:49
Monika: mam ja przyrownac do zera ?
30 lis 15:52
Monika: jest mniejsza od zera , tak ?
30 lis 15:52
J:
tak, czyli funkcja jest ...... ? w całej ........ ?
30 lis 15:54
Monika: mniejsza od zera funkcja jest
30 lis 16:06
J:
jaki przebieg ma funkcja, gdy pochodna jest ujemna ?
30 lis 16:07
Monika: jest malejąca
30 lis 16:08
J:
tak
30 lis 16:10
Monika: ale nie wiem w jakich przedziałach
30 lis 16:10
Monika: :(
30 lis 16:10
Monika: i nie wiem jakie są ekstrema
30 lis 16:11
J:
przecież sama napisałaś,że pochodna jest stale ujemna
30 lis 16:11
Monika: tak ale nie wiem co napisac w odpowiedzi ?
30 lis 16:12
J:
skoro funkcja jest malejąca w całej dziedzinie, to nie może mieć ekstremów
30 lis 16:13
Monika: aha ale w odpowiedzi jaka mam napisac odpowiedz ?
30 lis 16:14
J:
a jakie masz polecenie w zadaniu ?
30 lis 16:15
Monika: zbadać monotoniczność funkcji . ale mam pytanie czy nie moge tej pochodnej ktora mi wyszla
przyrownac do zera ?
30 lis 16:18
J:
spróbuj
30 lis 16:19
Monika: jesli pochodna jest ujemna to jest mniejsza od zera ?
30 lis 16:22
Monika: a jesli mam taki przykład 1/x * ex ?
30 lis 16:24
Monika: dziedzina jest równa r z wykluczeniem o , tak ?
30 lis 16:24
Monika: 0
30 lis 16:24
J:
tak
30 lis 16:27
Monika: i teraz licze pochodna
30 lis 16:29
Monika: pochodna wyszla xex−ex/x2 tak ?
30 lis 16:31
J:
a jaka jest dokładnie funkcja ?
30 lis 16:33
Monika: f(x) = 1
−−−−* ex a pochodna wyszla xex−ex
x −−−−−−−−−−−
x2
30 lis 16:45
Monika: nie wem czy to jest poprawne
30 lis 16:45
J:
| | ex(x − 1) | |
dobrze , tylko zapisz: y' = |
| |
| | x2 | |
30 lis 16:47
Monika: dobrze i teraz musze przyrownac do zera tak ?
30 lis 16:48
J:
tak
30 lis 16:48
Monika: czyli x1=1 ? i x2= 0 ?
30 lis 16:52
J:
a skąd 0 ?
30 lis 16:52
Monika: a nie czyli x1=1 tak ? i tylko jedno miejsce zerowe ?
30 lis 16:56
J:
dla x = 1 pochodna się zeruje , aby było ekstremum musi zmieniać znak w tym pinkcie
...zmienia ?
30 lis 16:58
Monika: nie rozumiem , od razu w szkole zapisujemy monotonicznosc o wypisaniu miejsc zerowych rysujemy
wykres i zaznaczymy przedziały
30 lis 17:00
J:
szukamy ekstremum...gdzie funkcja może mieć ekstremum ?
30 lis 17:01
Monika: funkcja ma ekstremum w punkcie x=1
30 lis 17:03
J:
a skąd wiesz ? może , ale wcale nie musi , jaki musi być spełniony warunek ?
30 lis 17:03
Monika: nie wiem
30 lis 17:07
J:
a no właśnie .. .ekstremum istnieje tylko wtedy, gdy pochodna zmienia znak
30 lis 17:08
Monika: aaha no tak a ta funkcja zmienia ?
30 lis 17:11
J:
nie funkcja tylko pochodna ! .. tutaj znak pochodnej zależy od wyrazenia: x − 1
czy ono zmienia znak w punkcie x = 1 ?
30 lis 17:16
Monika: taak zmienia z dodatniej na ujemna
30 lis 17:17
Monika: z malejacej na rosnaca
30 lis 17:17
J:
pochodna zmienia znak z ujemnego na dodatni, czyli funkcja najpierw maleje, a potem rośnie,
czyli w punkcie: x = 1 posiada ?
30 lis 17:19
Monika: tak posiada minimum lokalne w punkcie x=1
30 lis 17:22
Monika: i jest rosnaca od 1 do nieskonczonosci a jest malejaca od − nieskonczonosci do 1 , tak ?
30 lis 17:27
J:
OK.
30 lis 17:27
J:
hola , hola ..przecież x = 0 nie należy do dziedziny
30 lis 17:29
Monika: czyli dobrze wszystko jest ?
ale jeszcze mam pytanko jak mam min lokalne to wtedy pisze ze
funkcja osiaga minimum dla x=1 i to y tez podaje ?
30 lis 17:30
Monika: aha
czyli jaka jest odpowiedz prawidłowa ? skoro 0 nie naezy do dziedziny ?
30 lis 17:30
J:
trzeba sprawdzić, czy funcja posiada asymptotę pionową w x = 0
30 lis 17:33
Monika: nie miałam asymptot niestety
30 lis 17:36
J:
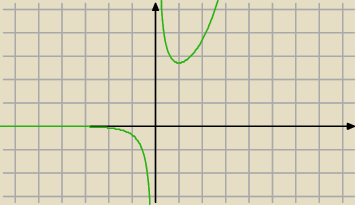
tutaj masz wykres ..
maleje w (−
∞,1)
rośnie w (1,+
∞)
minimum lokalne dla: x= 1 f
min = e
30 lis 17:41
Monika: aha dziekuje bardzo
30 lis 17:43
Monika: a jesli mialam taki przyklad gdzie dziedzina byla R/ √3 i −√3 to dlaczego odpowiedz jest ze
rosnie w przedizle od − pierwiastek z 3 do plus pierwiastek z 3 ?
30 lis 17:44
J:
a skąd mam to wiedzieć, jak nie widzę funkcji .. zapewne miała asymptoty w tych punktach
30 lis 17:50
Monika: funkcja byla x3/3−x2
30 lis 17:52
J:
fioletowe proste, to asymptoty pionowe
30 lis 17:55
Monika: funkcja jest rosnaca w przedzialach od −3 do − pierwiastek z 3 ; od −pierwiastek z trzech do
[ierwiastek z 3 i od pierwiastekz 3 do trzech ? a malejaca od − nieskonczonosci do −3 i od 3
do nieskonczonosci ? czy tak ?
30 lis 17:57
Monika: a jesli wyszly mi miejsca zerowe 0, −3,3 i wykluczam z dziedziny pierwiastek z 3 i −pierwiastek
z3 ? to wtedy jak powinien wyglądać wykres?
funkcja po obliczeniu wyszła x2(3−x)(3+x)
1 gru 08:12
J:
załóż nowy temat, bo już jest zamieszanie
1 gru 08:22