układ równań Asia: Pomoże ktoś w rozwiązaniu układu równań z czterema niewiadomymi? a² + b² = 25 c² + d² = 64 ac + bd = 20pierwiastek3 ad − bc = 20

Jack: ja na chłopski rozum zrobiłbym to tak a² = 25 − b² c² = 64 − d² czyli ac + bd = √25−b²* √64−d² + b*d = 20√3 ad − bc = analogicznie Jednakże troche tu liczenia by bylo, wiec na pewno da sie prosciej np. metoda Gaussa albo cos w tym stylu. Na pewno ktos inny wpadnie na lepszy pomysl

Asia: Próbuję na milion sposobów i jedynie kręcę się w kółko z tym wyznaczaniem czegoś i wstawianiem do czegoś... Chyba to jest ponad moje siły

+-: Trochę na zasadzie wróżenia z fusów (gdzieś jest √3), wynik wygląda na prawidłowy a=5 b=0 c=4√3 d=4

Mila: To jest ciąg dalszy jakiegoś zadania ?

AS: Wolfram podaje takie rozwiązanie b = −/+√25 − a² c = +/−4/5*(√25 − a² + a*√3) d = −/+4/5*(√3*√25 − a² + a)

Asia: Mila, tak, to zadanie jest z fizyki, ale układ równań na 100% mam dobrze zapisany. Wystarczy "tylko" rozwiązać − jak mawia pan profesor AS, dziękuję Tylko skąd to się krok po kroku wzięło...

AS: Tak na słowo honoru − bez gwarancji Przyjąłem na wiarę a = 3,b = 4 bo spełniają pierwsze równanie Wstawiając do 3−go i 4−go równania otrzymuję układ równań do rozwiązania 3*c + 4*d = 20*√3 3*d − 4*c = 20 Rozwiązaniem jest

	12*√3−16
c =
	5

	16*√3 + 12
d =
	5

Znalezione liczby spełniają wszystkie 4 dane równania,sprawdziłem. Może ten sposób pomoże rozwiązać podany problem, znając wejściowe dane a i b

Asia: Poświęciwszy na to zadanie kilka godzin każdego dnia, doszłam jedynie do wniosku: to zadanie ma baaaaaaaaaaardzoooooooo dużo rozwiązań. Dziękuję wszystkim za cudowną pomoc Dla ciekawych rozwiązania: Szkolnymi metodami nauki jest to nie do ogarnięcia, a przynajmniej zajmuje tyle czasu, że gdybym była na bezrobotnym, nie cierpiałabym na brak zajęcia. Matematyka na poziomie magisterki, chyba mnie nie kręci, aby ją poznać.

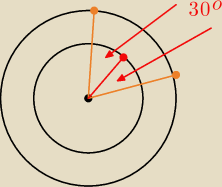
b.: To zadanie łatwo rozwiązać geometrycznie, kolejne warunki mają następującą interpretację: * (a,b) jest z okręgu o środku w (0,0) i promieniu 5, * (c,d) jest z okręgu o środku w (0,0) i promieniu 8, * iloczyn skalarny (a,b) i (c,d) wynosi 20√3, skąd wniosek, że kąt między tymi wektorami to +−U{π}[6}, * pole równoległoboku rozpiętego na (a,b), (c,d) wynosi 20 i to się zgadza z poprzednim warunkiem: pole wynosi 5*8*sin{π}{6}=20. Innymi słowy, ten warunek wynika automatycznie z poprzednich. Wobec tego każde rozwiązanie jest następującej postaci: za (a,b) bierzemy jakikolwiek punkt z okręgu o środku w (0,0) i promieniu 5, zaś za (c,d) jeden z dwóch punktów na okręgu o środku w (0,0) i promieniu 8, taki aby kąt między wektorami (a,b) i (c,d) wynosił +−π/6 i0

Asia: oooo jaaaaa.... SZACUN

b.: Przepraszam, jednak pomyłka: warunek ostatni jednak daje dodatkową informację, mianowicie ustala orientację tych dwóch wektorów (pomarańczowego i czerwonego na rysunku). Rozwiązaniami więc będą tylko takie (c,d), które leżą ,,na lewo'' od (a,b) −− czyli na rysunku tylko ten górny pomarańczowy punkt da rozwiązanie (ten z prawej dałby ad−bc=−20).