funkcja No_No: Dla jakich wartości parametru m równanie: −x² +3x+|x−4|=m ma jedno rozwiązanie ?

J: naszkicuj wykres

No_No: jak to zrobić jeżeli mam parametr?

J: Szkicujesz lewą stronę potem przesuwasz prostą y = m

No_No: Ok naszkicowałam: miejsca zarowe wyszły w punktach 1+√5 i 1−√5 dla x=1 funkcja przyjmuje największą wartość równą 5 i teraz m=5 ?

Mila: 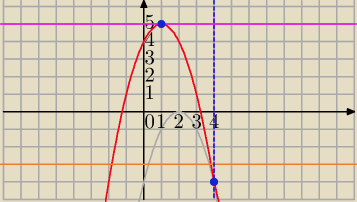−x² +3x+|x−4|=m Rysujemy wykres funkcji: f(x)=−x²+3x+|x−4| 1) |x−4|=x−4 dla x≥4 Wtedy f(x)=−x²+3x+x−4⇔ f(x)=−x²+4x−4⇔ f(x)=−(x−2)² dla x≥4 −−−−−−−−−−−−−−−−−−−−−−−−−−− 2) |x−4|=−x+4 dla x<4 f(x)=−x²+3x−x+4 f(x)=−x²+2x+4

	−2
xw=		=1
	−2

y_w=−1+2+4=5 −−−−−−−−−−−−−−−−−−−−−−−−−− Równanie : −x² +3x+|x−4|=m ma dla m<5 dwa rozwiązania dla m=5 jedno rozwiązanie dla m>5 brak rozwiązań.

PW: Prosta y = m przecina wykres (ma przecinać w jednym punkcie). Wykres to sklejone dwie funkcje kwadratowe na dwóch podzbiorach zbioru liczb rzeczywistych, określone jednym wzorem z użyciem wartości bezwzględnej − to masz narysować, a m może sobie wędrować dowolnie "góra−dół", bo jest parametrem.

No_No: ok, dzięki