okrąg gabson: Dany jest okrąg x²+y²=121. Jego cięciwa AB jest równoległa do osi OX i ma długość 20. Wyznacz współrzędne punktu P należącego do tej cięciwy, jeśli jego odległość od środka okręgu jest równa 5. i mam rozwiązanie takie: x²+y²=121 r=√121=11 S(0,0) −− współrzędne środka okręgu →10²+y²=11² y²=121−100 y=√21 −−− odległóść cięciwy AB od osi OX →5²=(√21)²+x² x²=25−21 x=2 −−−−odległość punktu P od osi OY ODP (√21 , 2) lub (√21 , −2) lub (−√21 , 2) lub (−√21 , −2) Czy mógłby mi ktoś wytłumaczyć te 2 działania oznaczone strzałkami? skąd biorą się do tego dane (szczególnie ta 10)

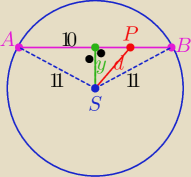
Eta: z tw. Pitagorasa y²= 11²−10² ⇒ y=√21 lu y= −√21 to punkt P(x,y) i S(0,0) i |SP|=d=5 d²= (x−0)²+(y−0)² ⇒ 25=x²+21 ⇒ x²=4 ⇒ x= 2 lub x=−2