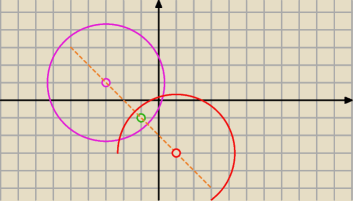
Wyznacz równanie okręgu Maciek: Dany jest okrąg O₁:x²+y²+6x−2y=0. Wyznacz równanie okręgu O₂ będącego obrazem okręgu O₁ w symetri względem punktu S(−1,−1)

===: (x+3)²+(y−1)²=10

Maciek: Przydało by się rozwiązanie ale bez rysunku

===: masz kanoniczną postać danego okręgu ...znasz zatem jego środek O₁ oraz r Przez S i O₁ poprowadź prostą i wyznacz na niej O₂ Równanie szukanego okręgu to już banał

Martyna :

Jolanta: Poczatek (x−a)²+(y−b)²=r² x²−2ax+a²+y²−2by+b²−r²=0 x²+y²+6x−2y=0 −2ax=6x −2by=−2y. a²+b²−r²=0 a=−3. b=1. (−3)²+1²=r² 10=r² (x+3)²+(y−1)²=10

Jolanta: Środek okręgu S₂ jest symetryczny do S₁względem punktu (−1,−1) Punkt (−1,−1) jest środkiem odcinka |S₁S₂|

	xS1+xS2		yS1+yS2
xs=		. ys=
	2		2

	−3+xS2		1+yS2
−1=		−1=
	2		2

−2=−3+x_S2. −2=1+y_S2 1=x_S2. −3=y_S2 S₂(1,−3) Odp. (x−1)²+(y+3)²=10

Jolanta: Środek okręgu S₂ jest symetryczny do S₁względem punktu (−1,−1) Punkt (−1,−1) jest środkiem odcinka |S₁S₂|

	xS1+xS2		yS1+yS2
xs=		. ys=
	2		2

	−3+xS2		1+yS2
−1=		−1=
	2		2

−2=−3+x_S2. −2=1+y_S2 1=x_S2. −3=y_S2 S₂(1,−3) Odp. (x−1)²+(y+3)²=10