Ostrosłupy
morela: Spośród ostrosłupów prawidłowych czworokątnych, których krawędź boczna ma długość 10, wybierz
ten, w którym pole przekroju płaszczyzną wyznaczoną przez środki dwóch sąsiednich krawędzi
podstawy i wierzchołek ostrosłupa, ma największe pole. Oblicz jego objętość.
Bardzo proszę o pomoc
29 lis 14:35
Jack:
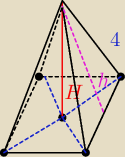
29 lis 15:52
Jack: zamiast 4 mialo byc 10... da sie tutaj edytowac rysunki?
29 lis 15:54
morela: Pomógł byś to rozwiązać? Nie potrafię policzyć

29 lis 15:56
Jack: @ Eta ?

29 lis 15:57
Jack:
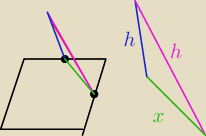
29 lis 16:02
Jack: Musimy obliczyć pochodną z pola i wyznaczyć takie długości boków by było Pole maksymalne,
(żeby podstawić do objętości).
29 lis 16:09
Jack:
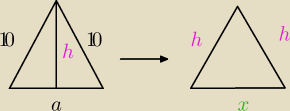
29 lis 16:12
Jack:
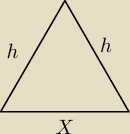
x właściwie wynosi : (1/2a)
2 + (1/2a)
2 = 1/2 a
2 =
12 * a
2
h (z pierwszego trójkąta) = 100 − 1/4a
2 = 100 −
14a
2
29 lis 16:19
Jack: Przepraszam za błąd...pitagoras nawet myli

X = pierwiastek z 1/2a
2 = pierwiastek 2/2 *a =
√22 * a
29 lis 16:21
morela: Ale z czego miałabym wyznać tą pochodną?
29 lis 16:22
Jack: Tu naprawdę przydałaby się możliwość edytowania...
Zacznijmy jeszcze raz
[post 16:12]
h2 = 102 − (1/2a)2
h = √100 − 1/2 a2
oraz iks, podany wyżej = √22 * a
29 lis 16:24
Jack:
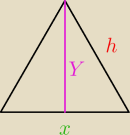
My chcemy, że pole tego trójkąta było jak największe.
29 lis 16:25
Jack: "h" mamy uzaleznione od "a"
oraz "x" mamy uzaleznione od "a"
a więc Pole tego trójkąta to jest :
P = 12 * x * Y
gdzie Y z Pitagorasa = h2 − (12 *x)2
29 lis 16:29
Eta:
| | a√2 | |
x= |
| −−− długość połowy przekątnej kwadratu o boku "a" |
| | 2 | |
29 lis 16:32
Jack: Przepraszam za tyle błędów... ehh
błąd w 16:24 −> h2 = 100 − 14 *a2
błąd w 16:29 −> Y2 = h2 − (12 * x)2
x2 = 12 * a2
a więc
Y2 = 100 − 18 * a2
Y = √100 − 18 * a2
P = 12 * √22 * a* √100 − 18 * a2
i teraz pochodną z tego...
29 lis 16:36
Jack: Pochodna :
P ' (a) = 400 − a2 / 4*√800−a2 = 400−a24* p{800−a2
29 lis 16:43
Jack: Miejsca zerowe pochodnej :
400 − a2 = 0
a2 = 400
a = 20 v a = −20
−20 nie spełniawarunków (a>0)
a więc Pmax jest największe dla a = 20
Czyli objętość...
29 lis 16:44
Jack: Nie znam wzoru ale znalazłem, że objętość
V = 13 * a2 * h
gdzie h − wysokość całego ostrosłupa
29 lis 16:47
Jack:
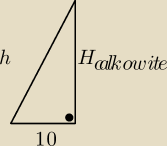
29 lis 16:50
Jack: i w tym momencie wszystko idzie w łeb...bo wychodzi , że Hmax = 0...
29 lis 16:55
Jack: daj mi chwile na sprawdzenie ... −.−
29 lis 16:57
morela: Dziękuję, że się starasz

Czekam
29 lis 17:02
Jack: No ewidentnie Pmax = 50 dla a = 20...
nie wiem gdzie mam błąd...Może nie to pole obliczyłem.
29 lis 17:14
Jack: Mamy obliczyć objętość całego ostrosłupa?
29 lis 17:17
Jack: W takim razie nie rozumiem polecenia...co to jest pole przekroju płaszczyzną wyznaczoną przez
środki dwóch sąsiednich krawędzi podstawy i wierzchołek ostrosłupa
29 lis 17:25
Jack: Ktoś inny mógł by się wypowiedzieć?
29 lis 17:30
Jack: @Eta?
29 lis 17:36
Jack: up
30 lis 19:00




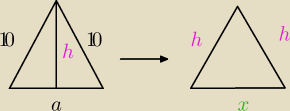
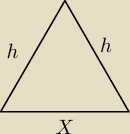 x właściwie wynosi : (1/2a)2 + (1/2a)2 = 1/2 a2 = 12 * a2
h (z pierwszego trójkąta) = 100 − 1/4a2 = 100 − 14a2
x właściwie wynosi : (1/2a)2 + (1/2a)2 = 1/2 a2 = 12 * a2
h (z pierwszego trójkąta) = 100 − 1/4a2 = 100 − 14a2
 X = pierwiastek z 1/2a2 = pierwiastek 2/2 *a = √22 * a
X = pierwiastek z 1/2a2 = pierwiastek 2/2 *a = √22 * a
 My chcemy, że pole tego trójkąta było jak największe.
My chcemy, że pole tego trójkąta było jak największe.
 Czekam
Czekam