półkole janko: Na średnicy półkola o promieniu długości r zbudowano trójkąt równoboczny o boku długości 2r. Obliczyć pole części trójkąta zawartej na zewnątrz półkola.

Jack:

Jack: P_Δ = ( (2r)²√3 ) / 4 = r²√3 P półkola = ¹₂*π*r² Dalej słucham innych?

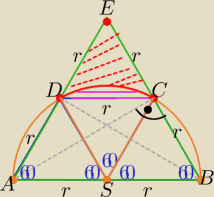Eta: P= P(ΔDCE) −P(odcinka DC koła)

	r2√3
P(ΔDCE)=
	4

	1
P(wycinka DCS koła)=		πr2
	6

	1		1		r2√3
to P=		πr2−P(ΔDCS)=		πr2−
	6		6		4

	r2√3		1		3r2√3−πr2		r2(3√3−π)
P= 2		−		πr2=		=		[j2]
	4		6		6		6

Jack: wlasnie o to mi chodzilo

Eta: