trygonomeria
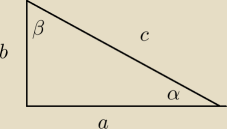
anekra43: Dla kątów ostrych α i β pewnego trójkąta prostokątnego zachodzi równość: sinα*sinβ=0,48.
Oblicz wartość wyrażenia cosα+cosβ.
28 lis 20:42
sushi_gg6397228:
i jaki masz pomysl na to zadanie ?
28 lis 20:45
Jack:
28 lis 20:47
anekra43: cosα+ cosβ= sinβ+sinα
28 lis 20:47
Jack: zgadza się...
28 lis 20:48
anekra43: tylko co dalej


28 lis 20:49
sushi_gg6397228:
to policz (sin α + sin β)2 =....
28 lis 20:49
anekra43: z podanej równości wyznaczyć można sinα i sin β ale nie wiem czy to się do czegoś może przydać
28 lis 20:50
anekra43: (sinα+sinβ)2 = 1,96
i wyłączyć pierwiastek z tego i tylko tyle ?
28 lis 20:51
sushi_gg6397228:
skad 1,96

mialas rozpisać ze wzorów skróconego mnożenia
28 lis 20:52
Jack: Zrób jak napisał : sushigg6397228: 20:52
apropos −> 0,48 2 ≠ 1,96
28 lis 20:56
anekra43: (sinα+sinβ)2 = sin2α + 2 sinαsinβ + sin2β= 2* 0,48 + sin2α + sin2β = 0,48+ 1 = 1,96
28 lis 20:56
sushi_gg6397228:
patrząc na zapis to jest beznadzieja, Ktoś kto się na tym nie zna, to jak zobaczy to
to bedzie sie zastanawiał skąd się wzięło sin2α, a powinno być sin2α
itp
trzeba kazde nowe "=" pisać od nowej linijki
28 lis 20:58
Jack:
(sinα+sinβ)2 = sin2α + 2 sinαsinβ + sin2β =
= sin2α + sin2β + 2*0,48
sin2α = 1−cos2α
28 lis 21:02
anekra43: Sorki za fatygę, widzę że u was pomocy nie otrzymam

Jack , no i wszystko się zgadza ,zamień sinα na cosα i będziesz miał jedynkę trygonometryczną !
28 lis 21:10
anekra43: *** zamień sinβ na cosα
28 lis 21:11
Jack: tak tak, w jakim sensie "u was pomocy nie otrzymam" ?
28 lis 21:56



 mialas rozpisać ze wzorów skróconego mnożenia
mialas rozpisać ze wzorów skróconego mnożenia
 Jack , no i wszystko się zgadza ,zamień sinα na cosα i będziesz miał jedynkę trygonometryczną !
Jack , no i wszystko się zgadza ,zamień sinα na cosα i będziesz miał jedynkę trygonometryczną !