wielomiany ~uczeń13: Pole trójkąta jest opisane wyrażeniem P(x)=6x³+18x²−2x−6, a jego podstawa − wyrażeniem a(x)=3x²−1. Wyraź wysokość opuszczoną na tę podstawę w zależności od x. Dla jakich x∊R dopuszczalna jest interpretacja funkcji P(x)?

Eta: x6x³+18x²−2x−6= 6x²(x+3)−2(x+3) = 2(x+3)(3x²−1) P(x) >0 ⇔ 6x³+18x²−2x−6>0 ⇔ 2(x+3)(3x²−1)>0

	√3		√3
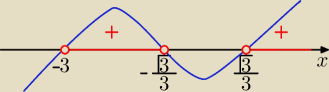
miejsca zerowe x=−3 v x=		v x= −		i rysujesz "falę"
	3		3

P(x)>0 ⇔ x∊(−3, −√3/3) U ( √3/3,∞)

	2P
i a(x)=3x2−1 2P=a*h ⇒ h(x)=		= ..... =4(x+3) , bo 3x2−1>0
	a

odp: h(x)=4x+12 dla x∊(−3, −√3/3) U ( √3/3, ∞)