funkcje, wykrasy, pomocy !! <prosi>!! Damian17: Sporządź wykresy funkcji i omów ich własności. 1)f(x)=²_x−2 2)f(x)= |⁻¹_x+1| +2 3)f(x)=^x_|x|−1 Proszę czy ktoś pomoże?

Damian17: wiem, że to pracochłonne zadanie, ale pojęcia nie mam jak to zrobić bo mnie nie było na lekcjach. nie było mnie ne tej lekcji, i mieli jeszcze przesunięcie tego wykresu ale to jest proste i sam z tym dam radę. Prosiłbym tylko bardzo o rozwiązanie tych przykładów

Damian17: Aaa i wiem że jest to do tematu, Funkcje homograficzne

Damian17: pomoże ktoś?

Damian17: proszę o pomoc...

Olusia: ale czego nie wiesz? Sporzadzic wykresu? Wybrac jakies x i podstawić do y? I taka mala podpowiedz do rysowania funcjji homograficznych jezeli a jest dodatnie ( w twoim przykladzie 1 to liczba 2) to wykres bedzie w 1 i 3 cwiartce. Natomiast jezeli jest ujemny to w 2 i 4. W przykladzie 1: 2 to asymptota pionowa. Poziomej w tym przykladzie nie ma. I tyle i rysujesz. Warto jeszce znalezc unkty przeciecia osiami wspolrzednych. O osią Ox za y podstawiasz 0 i obliczasz, z Osią Oy, za x podstawiasz 0 i obliczasz. W 2 przykladzie wartosc bezwzgledna kaze Ci odbic funkcje zeby nie bylo pod osia Ox.

Damian17: taa, fajnie bo ja dużo zrozumiałem

Damian17: dobra, i tak wiem że tego nie zrobię, postaram się na następne półrocze. Zawsze chodziłem do takiej pani i ona mi rozwiązywała, ale dzisiaj dopiero dostałem te przykłady a zaliczenia semesrtu są jutro Dobra odejdzie się bez..

Olusia: czego nie rozumiesz

Damian17: noo ale te własności? to co ja mam opisać, chociaż to żebym wiedział?

Olusia: a tak wogole ktora klasa jesteś? 3?

Damian17: aa czyli musi być jakiś wzór ogólny tak?

Damian17: 2 liceum

Damian17: ale mój nauczyciel nic nie tłumaczy, tylko zrobi 1 przykład na tablicy i zada nam ze zbiorów przykłady i musimy to robić

Olusia: ja w 3 liceum na poczatku mialam ta funkcje, w podreczniku wszystko jest pieknie wytlumaczone. A co do wlasnosci to nie wiem o co mu chodzilo. Moze o monotonicznosci. W 1 przykladzie funkcje jest malejąca

Damian17: noo a ja nie mam tego w książce, miałem na końcu I klasy średnią 4,8 i na pewno bym to znalazł w książce jeśliby było i nie prosiłbym o rozwiązanie tego zadania..

Olusia: To nie wiem jaki twoj nauczyciel prowadzi schemat uczenia, jak nie leci z tematen przeznaczonym na klase II. Ja w 3 na poczatku to mialem i chyba tam to powinno byc

Damian17: aa nie wiesz o co może mu chodzić z tymi własnośćiami?

Damian17: może jest ktoś kto mógłby mi to jeszcze tak inaczej spróbować wytłumaczyć, chcę zaliczyć ten semestr... Ale Tobie bardzo dziękuję, trochę mi podpowiedziałeś. no i te jakieś własności

Calineczka:): Chodzi mu o: dziedzine, zbiór wartości, miejsce zerowe, monotonicznosć, różnowartościowość, parzystość, okresowość. To są właśnie wartości funkcji

Calineczka:): Sorka Własności nie wartości

Bogdan: Jeśli należy przedstawić własności funkcji, to trzeba podać mi.in: 1. dziedzinę funkcji; 2. zbiór wartości; 3. monotoniczność; 4. znak funkcji (przedziały, w których funkcja dodatnia oraz przedziały, w których funkcja jest ujemna); 5. miejsca zerowe; 6. punkty przecięcia wykresu osi y; 7. ekstrema funkcji; 8. asymptoty (o ile istnieją); 9. parzystość, nieparzystość, okresowość, różnowartościowość. Można również podać różne postacie wzoru funkcji: np.: postać ogólną, postać kanoniczną, postać iloczynową (o ile istnieje).

Damian17: no dobrze to może bym to opisał, ale najpierw muszę to narysować

Bogdan: Tak, trzeba wykonać szkic wykresu funkcji

Damian17: miałem małą przerwę w szkole (miesiąc) i nie zbyt bardzo rozumiem

Olusia: Opisze Ci moze troche funkcje homograficzną Wzór ogolny to f(x)= a/x−p + q gdzie: jezeli a jest dodatnie wykres funkcji jest w 1 i 3 cwiartce jezeli a ujemne jest w 2 i 4 p − asymptota pionowa q− asymptopa pozioma Teraz mysle ze bez problemu narysujesz wykres 1

Damian17: oo noo już dużo lepiej, czyli sobie upraszaczam to co mam do tego ogólnego. DObra to tyle wiem. Aa co to są te asymptony, nie miałem nigdy tego

Damian17: aa czyli tak y=⁻¹_x +1+2

Damian17: ii później biorę samo ⁻¹_x i do tego podstawiam?

Olusia: Jak zes to uproscil Wartosc bezwzgl;edna opusciles? Asymptoty to miejsca w ktorych wykres funkcji nie moze wejsc. Rysuje sie je jako przerywane linie i te lini wykres nie moze przeciąc

Damian17: i rysuję funkcję? i jeżeli wartość bezwzględna ti zmieniam znaki w punktach z tej pierwszej?

Damian17: ten przykład robię |⁻¹_x+1 +2|

Bogdan: Do Olusi,

	a
f(x) = a/x − p + q czytamy f(x) =		− p + q. Należało zapisać:
	x

	a
f(x) =		+ q względnie f(x) = a / (x − p) + q.
	x − p

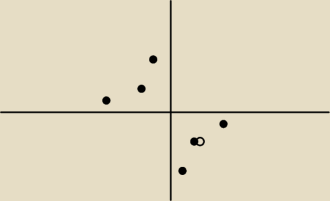
Damian17: coś takiego?

Damian17: Bogdan możę Ty byś mi pomógł?

Damian17: jest ktoś kto to potrafi to rozwiązać od A do Z, chociaż ten przykład |⁻¹_x+1 +2|

Bogdan: O który przykład Damianie pytasz?

Damian17: o ten Tutaj co napisałm wyżej

Bogdan: Stosuj dużą literkę U przy zapisywaniu ułamków. Czy w liczniku jest −1? Czy wartość bezwzględna obejmuje cały ułamek?

Damian17: tak tak to jest cała wartość bezwzględna wszytsko się tam znajduje

Damian17: i w liczniku jest "−1"

Bogdan:

	−1
f(x) = |		+ 2|
	x + 1

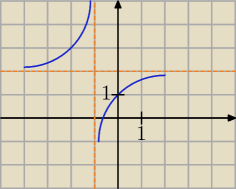
	−1
Najpierw trzeba narysować wykres y =		+ 2 (patrz rysunek).
	x + 1

Część wykresu znajdującą się pod osią x trzeba przerzucić (odbić) na drugą stronę tej osi,

	−1
powstanie wtedy wykres y = |		+ 2|
	x + 1

Damian17: aa czyli to "−1" i "+2" świadczy o przesunięciu wykresy tak?

Bogdan: Tak, wektor przesunięcia w = [−1, 2]

Damian17: aa no to troszkę zrozumiałem. czyli Df: (−4;−1) suma (−1;2)?

Damian17: wartośći (−1;2) suma (2;5)?

Damian17: jakie są jeszcze własności?

Bogdan: Nie. Dziedzina to: D_f: x∊R \ {−1}

Bogdan: Zbiór wartości ZW_f: y∊R \ {2}

Damian17: aa no tak to jest w wektora, dobrze myślę, rzeczywiste prócz tych z wektora

Damian17: są jeszcze jakieś własnośći dal tej funkcji?

Bogdan: Wymieniłem wcześniej w 9 punktach różne własności funkcji, trzeba je podać.

Damian17: aha już sobie z tym poradziłem wszystko jest dobrze Dzięki wielkie zrozumiałem to mniej więcej

Bogdan: Podaj monotoniczność, sprawdzę, czy tę własność umiesz dobrze zapisać. Chętnie zobaczyłbym pozostałe zapisane przez Ciebie własności.

Damian17: noo monotoniczność czyli dla jakich argumentów f rośnie czyli (−∞; +∞)\ {1} czy tak ?

Damian17: aa miałbym jeszcze pytanie, czy jeśli wartość bezwzględna będzie tylkko ułamek a ta "2" nie będzie w wartości to coś się zmieni?

Damian17: miejsce zerowe to −1

Bogdan: Monotoniczność jest źle zapisana.

Damian17: dodatnia od zera do +∞ \{−1} ujemna od −∞ do zera \{−1} czy tak?

Damian17: aa monotoniczność rośnie dla R\{−1} czy tak?

Damian17: przecięcie osi y to jest punkt 1

Bogdan:

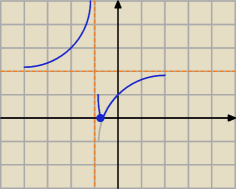
	−1
Tak wygląda wykres y = |		+ 2|
	x + 1

Bogdan: Monotoniczność, znak funkcji, miejsce zerowe − źle, podaj jeszcze raz.

Damian17: noo a tamten prędzej wykres to jest gdyby ta "2" stała za wartością bezwzględną tak?

Damian17: ale czy ona jest ciągła czy kończy się tak jak jest narysowane

Bogdan: A jak myślisz patrząc na wzór funkcji ?

Damian17: że jest ciągła?

Bogdan: Funkcja jest ciągła dla x∊D_f

Damian17: czyli tak rosnąca w przedziałach (−∞;0), (0;+∞) teraz dobrze?

Damian17: dla x⇒(−∞;0) przyjmuje wartości ujemne dla x∊(0;+∞) wartości dodatnie

Damian17: nie osiąga wartości najmniejszych ani największych

Damian17: aa osie układu są tymi asymptonami

Damian17: oj źle wartośći ujemne są od +∞; 0 aa ujemne od −∞; 0 na odwórt zrobiłem

Damian17: a dodatnie od −∞;0 **

Damian17: tak teraz mam rację? ;>

Bogdan:

	−1
Kombinuj dalej, na razie nie podałeś poprawnie własności funkcji f(x) = |		+ 2|.
	x + 1

Damian17: nie no ja wymiękam... potrzebuję własności dla obu tych funkcji f(x2|

	−1
f(x)=|		|+2
	x+1

bo nie jstem pewnien która będzie.. Proszę napisz mi...

Damian17:

	−1
aa ta druga to f(x)=|		+2|
	x+1

różnią się tylko tą wartością bezwzględną.. Napisz mi proszę..

Damian17: Bogdan naprawdę nie mam pojęcia... wiem że może dobrze kombinuje ale już mi pomysły uciekły jak to może być inaczej..

Damian17: trochę mi teraz namieszałeś... byłbym wdzięczny gdybyś mi podał własności ty obu funkcji które Ci napisałem. i tak już dużo wiem, jak narysować wiem, tylko własności nie potrafię wyznaczyć, ale byłbym wdzięczny...

AROB: Damianie jesteś jeszcze ? Chciałabym Ci pomóc.

Anna: Narysuj wykres funkcji f(x)= −3/x dla a ≠o i omów własnosci tej funkcj na podstawie wykresu. POmocy PILNI

5-latek : Prosze zalozyc nowy temat