Dany jest kwadrat o boku a= 6. W ten kwadrat wpisano trójkąt równoboczny w ten sposób, że
jeden wierzchołek trójkąta jest wierzchołkiem kwadratu, a przeciwległy bok trójkąta jest
równoległy
do przekątnej kwadratu (patrz rysunek). Wykaż, że bok trójkąta jest równy 6( √6 −√2).
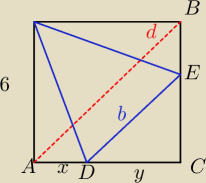62+x2=b2
d=6√2
trójkąty ABC i DEC są podobne więc możemy ułożyć proporcje
| y | b | ||
= | |||
| 6 | 6√2 |
| 5^2 | 52 |
| 2^{10} | 210 |
| a_2 | a2 |
| a_{25} | a25 |
| p{2} | √2 |
| p{81} | √81 |
| Kliknij po więcej przykładów | |
|---|---|
| Twój nick | |