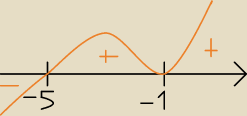Zbadaj monotonicznośd i ekstrema funkcji
Maura:
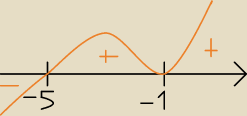
| | (x−1)3 | |
f(x)= |
| Df=R \ {−1} |
| | (x+1)2 | |
| | (x−1)2(x+5) | |
Pochodna wyszła mi: f'(x)= |
| |
| | (x+1)3 | |
Przyrównuję pochodną do zera i wychodzi x=−1 nie należy do dziedziny oraz x=−5
Rysuję wykres jw. i wychodzi, że jest malejąca x∊(−
∞,−5) a rosnąca w x∊(−5,−1), x∊(−1,
∞)
Co robię źle bo odpowiedź to:
f rosn. dla x∊(−
∞,−5) oraz x∊(−1,
∞)
f malejąca dla x∊(−5,−1)
Proszę pomóżcie

27 lis 18:37
irena_1:
f'(x)>0, jeśli (x−1)2(x+1)3(x+5)>0
Zapomniałeś o znaku mianownika
27 lis 18:54
Eta:
x≠−1
f'(x)>0 to f(x) ↗ ⇔ (x+1)3(x−1)2(x+5)>0 ⇔ (x+1)(x+5)>0 i x≠ −1 ⇔ x∊(−∞,−5)U (−1,∞)
f(x)↘ ⇔x∊(−5,−1)
27 lis 18:57
Maura: (x−1)2(x+1)3(x+5)>0 dlaczego wszystko jest przez siebie przemnożone? w każdym przykładzie tak
trzeba robić?
27 lis 19:33