Potrzebuję pomocy przy 2 zadaniach. Krystian: 1. Rozwiąż równanie. Odpowiedź podaj w radianach: a) sin2x − 2sinx = 0 b) sin2x + 3cosx = 0 c) cos2x + sin ²x = 1 d) cos²x = cos2x e) cos2x = 2sin²x 2. Rozwiąż równanie. Rozwiązanie podaj w stopniach. a) cos2x = sin x Każdy przykład mam zaczęty, w większości mam odpowiedzi, ale nie jestem ich pewien dlatego proszę o pomoc i rozwiązanie tych równań.

Frost: Podaj odpowiedzi; sprawdzimy

Krystian: 1. a) kπ

	π
b)		+ kπ
	2

c) kπ d) kπ e) nie mam 2. a) nie mam

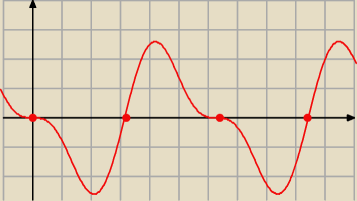
Janek191: Np. a) 2 sin x*cos x − 2 sin x = 0 2 sin x*( cos x − 1) = 0 sinx = 0 lub cos x = 1 x = π*k lub x = 2π*k , k − dowolna liczba całkowita Krócej: x = π*k ============ Patrz też na wykres:

Janek191: 2 a) 1 − 2 sin² x = sin x 2 sin² x + sin x − 1 = 0 Dokończ

Eta: Nie chce mi się

Krystian: A mogę liczyć na samo rozpisanie kolejnych przykładów ?

Janek191: 1 e) 1 − 2 sin² x = 2 sin² x 4 sin² x = 1

	1
sin2 x =
	4

	1		1
sin x = −		lub sin x =
	2		2

Krystian: Prosiłbym o rozpisanie 1 b) c) d) i 2 a)

Janek191: 1 b) 2 sin x*cos x + 3 cos x = 0 cos x*( 2 sin x + 3) = 0 cos x = 0 bo 2 sin x + 3 > 0

	π		π
x =		+ 2π*k lub x = −		+ 2π*k
	2		2

	π
Krócej: x =		+ π*k
	2

====================

Janek191: 1 c) 1 − 2sin² x + sin² x = 1 − sin² x = 0 sin x = 0 x = π*k , k − dowolna liczba całkowita

Janek191: 1 d) cos² x = 2 cos² x − 1 cos² x = 1 cos x = − 1 lub cos x = 1 x = − π + 2π*k lub x = π + 2π*k Krócej: x = k*π ======

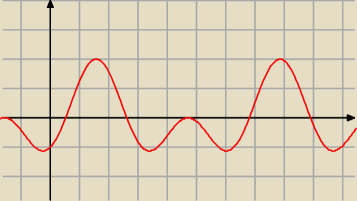
Janek191: cd. 2 a) 2 sin² x + sin x − 1 = 0 Δ = 1 − 4*2*(−1) = 9

	−1 − 3		− 1 + 3
sin x =		= − 1 lub sin x =		= 0,5
	4		4

	π		π		5
x = −		+ 2π*k lub x =		+ 2π*k lub x =		π +2π*k
	2		6		6

Krystian: Skąd wzięły się te wyniki w zad 2 ?

Krystian: Wiem tyle że ma wyjść x=270 stopni, 30 stopni i 150 a nie wychodzi mi...

Janek191:

	π
−		= −90o
	2

− 90^o + 1*360^o = 270^o

π
	= 30o
6

5		5
	π =		*180o = 150o
6		6

Janek191: Pewnie miałeś rozwiązać równania w < 0 ; 2π > = < 0^o, 360^o >