Oblicz granicę funkcji.
Solpek: Bardzo proszę o pomoc w rozwiązaniu... Jestem kompletnie zielona
lim √x2+1 − √x+1 / 1 − √x+1
x→0
Całe wyrażenia typu x+1 są pod pierwiastkiem
27 lis 17:29
Janek191:
| | √x2 + 1 − √x + 1 | |
f(x) = |
| ? |
| | 1 − √x +1 | |
27 lis 17:40
Janek191:
Stosujemy wzór:
do licznika i do mianownika.
27 lis 17:42
Solpek: Dokłądnie tak ma to wyglądać. I tak nie wiem co mam dalej z tym wzorem począć.
27 lis 17:44
Janek191:
| | | x2 + 1 − (x +1) | |
| | | √x2 + 1 +√x +1 | |
| |
f(x) = |
| = |
| | | |
| | x*(x − 1) | | 1 + √x +1 | |
= |
| * |
| = |
| | √x2 + 1 + √x +1 | | − x | |
| | (1 − x)*( 1 +√ x +1) | |
= |
| |
| | √x2 +1 + √x +1 | |
więc
| | 1*( 1 + 1) | |
lim f(x) = |
| = 1 |
| | √1 +√1 | |
x→0
27 lis 17:48
Solpek: Dzieki wielkie. Mozesz z jeszcze jednym pomóc?
lim x − 5 / √x − 1 − 2
x→5
27 lis 17:57
Janek191:
| | x −5 | | x −5 | |
f(x) = |
| = |
| = |
| | √x −1 − 2 | | | |
| | √x −1 + 2 | |
= (x −5)* |
| = √ x −1 + 2 |
| | x − 5 | |
więc
lim f(x) =
√ 5 − 1 + 2 = 2 + 2 = 4
x→5
27 lis 18:10
Janek191:
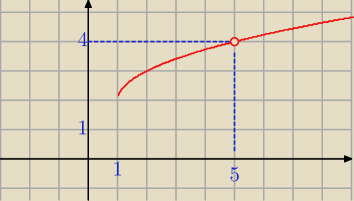
27 lis 18:12
Solpek: Dziękuję bardzo <3
27 lis 19:09
