Geometria płaszczyzny
Ania:
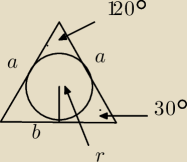
Na okręgu o promieniu 3 opisano trójkąt równoramienny o kącie między ramionami 120. Oblicz
długości boków tego trójkąta.
Nie rozumiem tego zadania, zrobiłam tylko rysunek i nie wiem co dalej robić.
Pomoże ktoś ?
26 lis 18:31
Domanika:
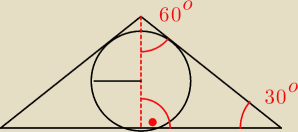
Znasz zależności trójkąta o stopniach 30
o, 60
o i 90
o?
26 lis 18:46
Domanika:
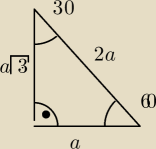
26 lis 18:50
Domanika: Nie. Po przemyśleniu to nic nie da... Przepraszam, że wprowadziłam w błąd.
26 lis 19:35
Janek191:
L = a + 2 b
P = 0,5 L*r = 0,5 L*3 = 1,5 L = 1,5 ( a + 2 b)
| | √3 | |
P = 0,5 b2*sin 120o = 0,5 b2* |
| = 0,25 √3 b2 |
| | 2 | |
| 0,5a | | √3 | |
| = cos 30o = |
| ⇒ a = b√3 |
| b | | 2 | |
zatem
P = 1,5*( b
√3 + 2 b) = 1,5 b*(
√3 + 2)
P = 0,25
√3*b
2
czyli
1,5 b*(
√3 + 2) = 0,25
√3*b
2 / * 4
6 b*(
√3 + 2) =
√3 b
2 / : b
6
√3 + 12 =
√3 b / :
√3
6 + 4
√3 = b
==========
a = b
√3 = ( 6 + 4
√3)*
√3 = 6
√3 + 12
=================================
Oznaczenia:
a − długość podstawy Δ równoramiennego
b − długość ramion
26 lis 19:56
Eta:
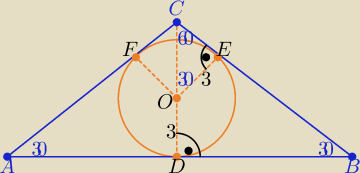
|OC|=2
√3 , |CD|=3+2
√3
to |BC|= 2(3+2
√3) i |DB|= (3+2
√3)*
√3 = 3
√3+6=3(
√3+2)
to |AB|= 2|DB|= 6(
√3+2)
26 lis 19:57
Eta:

26 lis 19:58
Janek191:
Eta jak zwykle pięknie

26 lis 20:34
Eta:

26 lis 20:34
Eta:
Ciekawe gdzie jest właścicielka tego postu?
przepisała ...... i...........
26 lis 21:38
===:
... trzeba zacząć ignorować jej zadanka .. jeszcze nie widziałem aby podziękowała komukolwiek
27 lis 21:18
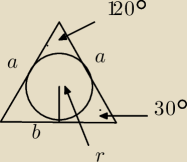 Na okręgu o promieniu 3 opisano trójkąt równoramienny o kącie między ramionami 120. Oblicz
długości boków tego trójkąta.
Nie rozumiem tego zadania, zrobiłam tylko rysunek i nie wiem co dalej robić.
Pomoże ktoś ?
Na okręgu o promieniu 3 opisano trójkąt równoramienny o kącie między ramionami 120. Oblicz
długości boków tego trójkąta.
Nie rozumiem tego zadania, zrobiłam tylko rysunek i nie wiem co dalej robić.
Pomoże ktoś ?
 Znasz zależności trójkąta o stopniach 30o, 60o i 90o?
Znasz zależności trójkąta o stopniach 30o, 60o i 90o?

 |OC|=2√3 , |CD|=3+2√3
to |BC|= 2(3+2√3) i |DB|= (3+2√3)*√3 = 3√3+6=3(√3+2)
to |AB|= 2|DB|= 6(√3+2)
|OC|=2√3 , |CD|=3+2√3
to |BC|= 2(3+2√3) i |DB|= (3+2√3)*√3 = 3√3+6=3(√3+2)
to |AB|= 2|DB|= 6(√3+2)


