Działania na zbiorach, wykaż Koleżanka: Pomoże ktoś, w wykazaniu, że... ? Bo chyba utknęłam A∪(B\A) = A∪B _df.∪ A∪(B\A) ⇔ x∊A ∨ x∊(B\A) df \ ⇔ x∊A ∨ (x∊B ∧ x∉A) rozdz. altern. wzgl. koniunk. ⇔ (x∊A ∨ x∊B) ∧ (x∊A ∨ x∉A) ⇔ ? ? ↑ nie wiem jak się mam tego pozbyć

Koleżanka: nikt? :< wiekszosc zrobilam tylko koncowki nie umiem

Tadeusz: patrz w podpunkcie b) https://matematykaszkolna.pl/strona/2883.html

Koleżanka: nie bardzo mi to pomoglo

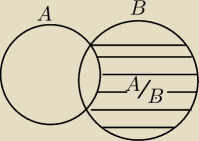
J: może tak:

J: tam ma być: B/A

ICSP: ⇔ x ∊ A v x ∊ B ⇔ x ∊ A∪B

Koleżanka: ja wiem co to jest przeciez B\A tylko ze ja to mam wykazać za pomocą df i praw logicznych. Ale mi wyszlo ze x nalezy do A lub x nie należy do A i musze się tego pozbyć, a nie wiem jak. Tylko o to mi chodzi..... df.∪ A∪(B\A) ⇔ x∊A ∨ x∊(B\A) df \ ⇔ x∊A ∨ (x∊B ∧ x∉A) rozdz. altern. wzgl. koniunk. ⇔ (x∊A ∨ x∊B) ∧ (x∊A ∨ x∉A) ⇔ ? ?

Koleżanka: noo wreszcie ktoś mi odpowiedzial Dzięki ICSP Czyli mi to po prostu znika tamto?

qbar: Chyba z prawa wyłączonego srodka sie tego po prostu pozbywasz, bo to jakby jest zawsze prawdą

ICSP: Znika.

Koleżanka: Dziękuje bardzo