Zbyt trudne zadanie? Kraterek: Poniższe zadanie jest banalne (no może nie takie banalne, ale nie bardzo trudne) do zrobienia dla licealisty. Jednak otrzymał je uczeń gimnazjum. Mam pytanie, czy ktoś ma pomysł jak zrobić je właśnie na poziomie gimnazjalnym, bez znajomości twierdzenia Talesa i bez równania kwadratowego? Czy jest to w ogóle możliwe? Oto treść: Na działce w kształcie trójkąta równobocznego o boku 6 m zrobiono prostokątny klomb kwiatowy o największym z możliwych polu. Pozostałą część działki stanowi trawnik. Oblicz pole trawnika.

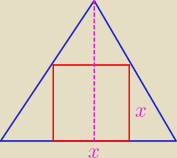
Janek191: h − wysokość Δ równobocznego

	6 √3
h = U{a√3{2} =		= 3 √3
	2

Z podobieństwa trójkątów mamy

h − x		h
	=
x		6

h*x = 6*( h − x) = 6 h − 6 x h*x + 6 x = 6 h x*( h + 6) = 6 h

	6 h		6*3√3		18√3		6√3
x =		=		=		=		=
	h + 6		3√3 + 6		3*(√3 + 2)		√3 + 2

	6√3*( 2 −√3)
=		= 12 √3 − 18
	(2 + √3)*(2 −√3)

więc pole kwadratu P_k = x² = ( 12 √3 − 18)² = 144*3 − 432√3 + 324 = 756 − 432√3 Pole trawnika

	62 √3
P =		− ( 756 − 432 √3) = U{36√3}{4{ − ( 756 − 432√3) = 9√3 − (756 −
	4

432√3) = =441√3 − 756 ≈ 7,83 P ≈ 7,83 m² ==========

J: Janek ... jak gimnazjalista ma uzasadnić,ze najwieksze pole bedzie miał kwadrat ?

Kraterek: Dzięki, rozwiązanie sensowne, ale opiera się na przekonaniu, ze prostokątem o największym polu będzie kwadrat. Jak słusznie zauważył J, skąd gimnazjalista ma to wiedzieć... Mnie się wydaje, że w praktyce jest to zadanie nie do rozwiązania na poziomie gimnazjum.