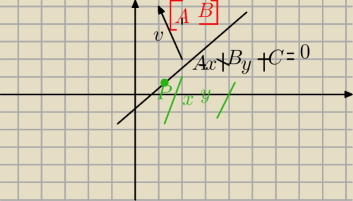
Proste i rownania 5-latek: Chciałbym wrocic jeszcze do rownan prostych w postaci ogolnej mamy wektor v=[A B] jest on prostopadly do prostej Ax+By+c=0 Prosta ta przechodzi przez punkt P=(x,y) czyli jeśli mamy podany wektor v=[A B] o znanych wspolrzednych A i B to możemy napisac równanie prostej prostopadlej do tego wektora i przechodzącej przez punkt P czyli równanie Ax+By+c=0 Teraz jeśli mamy podane równanie prostej Ax+By+C=0 i mamy napisac równanie prostej prostopadlej do niej to dlaczego to równanie ma postac −Bx+Ay+C=0 ? Ja się domyślam z etu chodzi o iloczyn skalarny wektorow ze musi być rowny 0 najpierw chciałby wyjasnic proste prostopadle , a potem proste rownolegle

5-latek: Jeśli chodzi o równanie prostej rownoleglej do prostej Ax+By+C=0 i przechodzącej przez punkt P to to równanie będzie miało postac A(x−x₀)+B(y−y₀)+C=0

Mila: 1) Dla dowolnego D∊R prosta: Bx−Ay+D=0 jest prostopadła do prostej Ax+By+C=0 a także: Dla dowolnego D∊R prosta −Bx+Ay+D=0 jest prostopadła do prostej Ax+By+C=0 Iloczyn skalarny wektorów: [B,−A], [A,B] B*A+(−A)*B=0 i (−B)*A+A*B=0 2) Przykład : k: 2x+5y+4=0 m: 5x−2y+D=0 prosta m⊥k dla dowolnego D∊R np: 5x−2y+1=0, D=1 5x−2y−6=0, D=−6 −5x+2y−6=0

Mila: Postać ogólna równania prostej Ax+By+C=0 2) Dla dowolnego D∊R prosta Ax+By+D=0 jest równoległa do prostej Ax+By+C=0 Przykład: k: 2x+5y+4=0 m: 2x+5y+D=0 prosta m||k dla dowolnego D∊R

5-latek: Dobry wieczor Milu Pozdrawiam Czyli dobrze z tym iloczynem skalarnym . Natomiast nie wzialem pod uwagę zamiany wspolrzednych wektora (tzn jedna tak ale drugiej nie . dziekuje CI

5-latek: Teraz już nie będzie zadnych wątpliwości

Mila: Jak ręka?

5-latek: Jednak był zastrzyk . Do poniedziałku mam zwolnienie jeszcze . Dostalem skierowanie tez do ortopedy ale już miejsca do końca roku nie ma Nie wiem może pojde prywatnie (110zl wizyta i niewiadomo czy przyjmie