Równania trygonometryczne
Robert: Rozwiąż równanie. Podaj najmniejszą liczbę z przedziału (3;+∞) spełniającą to równanie.
a) tgx=−√33
Wiem, że jest już takie zadanie natomiast nie zrozumiałem go do końca. Tangens przyjmuje taką
wartość dla dwóch kątów 150* i 330*. Skąd mam wiedzieć, do którego się odnieś?
24 lis 20:39
Janek191:
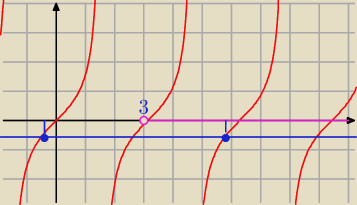
======================
24 lis 20:50
Robert: A do −π6 doszedłeś przemieniając na procenty. Skąd mam wiedzieć, że to będzie 330* a nie
150*
24 lis 20:55
Eta:
| | π | | 5 | | 5*3,14 | |
dla k= 1 x= − |
| +π= |
| π≈ |
| ≈2,62 <3 −− odpada |
| | 6 | | 6 | | 6 | |
| | π | | 11 | | 11*3,14 | |
dla k=2 x= − |
| +2π= |
| π≈ |
| ≈5,76>3 |
| | 6 | | 6 | | 6 | |
24 lis 21:00
Janek191:
Stopnie, a nie procenty. Pewnie jesteś po procentach i słabo myślisz

Ma być : x > 3
| | 150 | |
a 150o = |
| *π ≈ 2,6 < 3 |
| | 180 | |
24 lis 21:01
Robert: Dzięki, że pomagacie. Natomiast skąd wiesz, że x=−π6?
24 lis 21:02
Janek191:
| | √3 | |
tg ( − 30o} = − tg 30o = − |
| |
| | 3 | |
24 lis 21:04
Janek191:
| | √3 | |
tg ( − 30o} = − tg 30o = − |
| |
| | 3 | |
24 lis 21:04
Robert: Nie dzisiaj

Dobra rozumiem, wstawiłem przed twoim komentarzem. Zyczę miłej nocki

24 lis 21:04
Eta:
| | π | | π | | √3 | |
tg(− |
| )=− tg |
| = − |
| |
| | 6 | | 6 | | 3 | |
24 lis 21:04
Robert: Mam jeszcze jedno pytanie, bo za cholere nie wiem skąd to bierzecie. Mam na myśli @Eta twój
ostatni komentarz.
24 lis 21:10

 Ma być : x > 3
Ma być : x > 3
 Dobra rozumiem, wstawiłem przed twoim komentarzem. Zyczę miłej nocki
Dobra rozumiem, wstawiłem przed twoim komentarzem. Zyczę miłej nocki 