a
Hedonista: Rozwiąż algebraicznie
|x−y|=2
|x+y|=4
rozpisując wyszło mi:
x=−3, y=−1 dla |x−y|<0, |x+y|<0 oraz |x−y|>0, |x+y|<0
x=3, y=1 dla |x−y|>0, |x+y|>0 oraz |x−y|<0, |x+y|>0
Pytanie brzmi które to są dobre rozwiązania?
2zadJak to w ogóle rozpisać?
|x+y|<5
|x−y|=>(większylubrówny)1
24 lis 20:37
Hedonista: up
24 lis 20:52
Hedonista: up
28 lis 19:03
Hedonista: up
28 lis 20:04
Mila: Masz rozwiązać taki układ równań?
|x−y|=2,
|x+y|=4
28 lis 20:12
Jack: są 4 układy i każdy jest rozwiązaniem
1)
|x−y|<0
|x+y|<0
2)
|x−y|<0
|x+y|>0
3)
|x−y|>0
|x+y|<0
4)
|x−y|>0
|x+y|>0
28 lis 20:16
Jack: 1)
x−y = −2 −> x = −2+y
x+y = −4
a więc :
−2+y +y = −4
2y = −2
y=−1
x= −2−1 = − 3
Rozwiązanie : y= − 1 x=−3
Kolejne układy tak samo...
28 lis 20:20
Jack: zad 2.
|x+y|<5
|x−y|≥1
Znowu rozbijasz na układy...
28 lis 20:22
Hedonista: okej czaję, właśnie się za to zabieram.
28 lis 20:27
Mila:
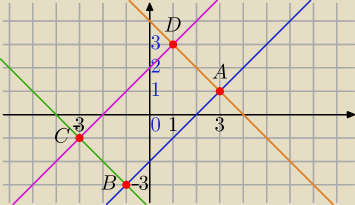
1) |x−y|=2⇔
x−y=2 lub x−y=−2⇔
y=x−2 lub
y=x+2 proste równoległe , nie przecinają się
2) |x+y|=4⇔x+y=4 lub x+y=−4⇔
y=−x+4 lub y=−x−4 proste równoległe , nie przecinają się
Zatem szukamy punktów wspólnych prostych przecinających się:
Patrz rysunek:
a)
x−y=2
x+y=4
−−−−−−−−−
2x=6⇔ x=3 iy=1 A:
x=3 i y=1
b)
x−y=2
x+y=−4
−−−−−−−−
2x=−2 ⇔x=−1 i y=−3 B:
x=−1 i y=−3
c)
x−y=−2
x+y=−4
−−−−−−−−
2x=−6, ⇔x=−3 i y=−1 C:
x=−3 i y=−1
d)
x−y=−2
x+y=4
−−−−−−
2x=2⇔x=1 i y=3 D:
x=1 i y=3
28 lis 21:19
Hedonista: thx wszystko ładnie rozpracowane

28 lis 21:59
J:

dla
Mili
28 lis 22:09
Mila:
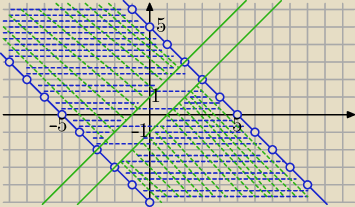
Zadanie2.
|x+y|<5⇔
−5<x+y<5 /−x⇔
−5−x<y<5−x
obszar między prostymi y=−x−5 i y=−x+5
i
|x−y|≥1⇔
x−y≤−1 lub x−y≥1⇔
x+1≤y lub x−1≥y ⇔
y≥x+1 obszar na prostej
y=x+1 i nad prostą
lub
y≤x−1 obszar na prostej
y=x−1 i pod prostą
Rozwiązanie− część wspólna zielonego i niebieskiego obszaru.
28 lis 22:41
 1) |x−y|=2⇔
x−y=2 lub x−y=−2⇔y=x−2 lub y=x+2 proste równoległe , nie przecinają się
2) |x+y|=4⇔x+y=4 lub x+y=−4⇔y=−x+4 lub y=−x−4 proste równoległe , nie przecinają się
Zatem szukamy punktów wspólnych prostych przecinających się:
Patrz rysunek:
a)
x−y=2
x+y=4
−−−−−−−−−
2x=6⇔ x=3 iy=1 A: x=3 i y=1
b)
x−y=2
x+y=−4
−−−−−−−−
2x=−2 ⇔x=−1 i y=−3 B: x=−1 i y=−3
c)
x−y=−2
x+y=−4
−−−−−−−−
2x=−6, ⇔x=−3 i y=−1 C: x=−3 i y=−1
d)
x−y=−2
x+y=4
−−−−−−
2x=2⇔x=1 i y=3 D: x=1 i y=3
1) |x−y|=2⇔
x−y=2 lub x−y=−2⇔y=x−2 lub y=x+2 proste równoległe , nie przecinają się
2) |x+y|=4⇔x+y=4 lub x+y=−4⇔y=−x+4 lub y=−x−4 proste równoległe , nie przecinają się
Zatem szukamy punktów wspólnych prostych przecinających się:
Patrz rysunek:
a)
x−y=2
x+y=4
−−−−−−−−−
2x=6⇔ x=3 iy=1 A: x=3 i y=1
b)
x−y=2
x+y=−4
−−−−−−−−
2x=−2 ⇔x=−1 i y=−3 B: x=−1 i y=−3
c)
x−y=−2
x+y=−4
−−−−−−−−
2x=−6, ⇔x=−3 i y=−1 C: x=−3 i y=−1
d)
x−y=−2
x+y=4
−−−−−−
2x=2⇔x=1 i y=3 D: x=1 i y=3

 dla Mili
dla Mili
 Zadanie2.
|x+y|<5⇔
−5<x+y<5 /−x⇔
−5−x<y<5−x obszar między prostymi y=−x−5 i y=−x+5
i
|x−y|≥1⇔
x−y≤−1 lub x−y≥1⇔
x+1≤y lub x−1≥y ⇔
y≥x+1 obszar na prostej y=x+1 i nad prostą
lub
y≤x−1 obszar na prostej y=x−1 i pod prostą
Rozwiązanie− część wspólna zielonego i niebieskiego obszaru.
Zadanie2.
|x+y|<5⇔
−5<x+y<5 /−x⇔
−5−x<y<5−x obszar między prostymi y=−x−5 i y=−x+5
i
|x−y|≥1⇔
x−y≤−1 lub x−y≥1⇔
x+1≤y lub x−1≥y ⇔
y≥x+1 obszar na prostej y=x+1 i nad prostą
lub
y≤x−1 obszar na prostej y=x−1 i pod prostą
Rozwiązanie− część wspólna zielonego i niebieskiego obszaru.