W trójkącie ABC dane są: wierzchołek A (2, -4) i równania trzech środkowych
jba: Nie mogę sobie poradzić z tym zadaniem kompletnie
W trójkącie ABC dane są: wierzchołek A (2, −4) i równania trzech środkowych
4x+y−6=0
2x+y−2=0
x−2=0
Znajdź równania boków tego trójkąta.
24 lis 19:33
Tadeusz:
1) Sprawdź do której z tych prostych należy punkt A
2) wykorzystaj fakt, że środkowe przecinają się w jednym punkcie i punkt ten dzieli je
w stosunku 2:1
24 lis 20:04
Tadeusz:
i wpisuj dokładnie treść zadań ... na pewno nie "znajdź równania boków"

24 lis 20:05
jba: To już zrobiłem, wyznaczyłem też punkt przecięcia środkowych i środek boku BC, ale nie wiem co
zrobić dalej
24 lis 20:09
Tadeusz:
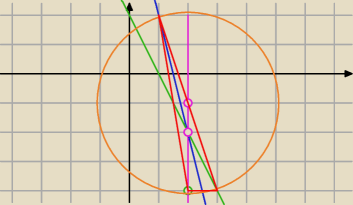
24 lis 21:25
Tadeusz:
A policzysz to tak:
Znasz wierzchołek A=(2,−4)
środek ciężkości S=(2, −2)
środek boku BC D=(2,−1)
Piszesz równanie pęku prostych przez punkt D
y+1=a(x−2) ⇒ y=ax−2a−1
Szukasz współrzędnych punktów przecięcia tej prostej z prostymi zawierającymi środkowe czyli:
ax−2a−1=−4x+6 ax−2a−1=−2x+2
x(a+4)=2a+7 x(a+2)=2a+3
| | 2a+7 | | 2a+3 | |
xC= |
| xB= |
| |
| | a+4 | | a+2 | |
| | xB+xC | |
Wiedząc, że |
| =2 wyznaczysz a=−3 |
| | 2 | |
... a dalej już x
C=1 x
B=3
y
C=2 y
B=−4
24 lis 22:49

