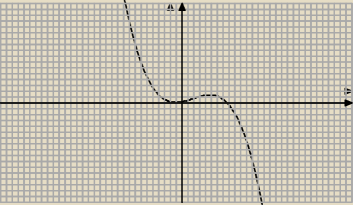
wykres funckcji Sylwia: Proszę o sprawdzenie −bo już nie daję rady funkcja x²−x³ narysować funkcje itd D ∊ R x²(1−x) = 0 punkty zerowe to X=0 i x=1 f(0)= 0 punkty 0Y = (0,0) monotoniczność f ' < 0 gdy x > ²₃ czyli x∊ (²₃; +∞) i x< 0 czyli x∊(−∞;0) f '> 0 gdy x<²₃ i x>0 czyli x∊ (0;²₃) ekstremum f '(x) =0=²₃ f(0)=⁴₂₇ lim tu zaczynają się schody czy granica x²−x³ przy x →+∞ = −∞ a przy x →−∞ = +∞ tak czy owak są różne czyli asymptoty poziome nie istnieją pionowe też bo D∊ R a ukośne nie istnieją bo granice nie są liczbami rzeczywistymi Bo ^f(x)_x =x−x² a granica to ile wynosi przy x →+∞

	2
licząc pochodną wiemy że x=		i x= 0
	3

czy ja dobrze to rozumuję ? f(x) jest wypukła gdy f '' >0 u nas f " = 2−6x czyli f " > ¹₃ ? f(x) jest wklęsła gdy f '' <0 u nas f " = 2−6x czyli f " < ¹₃ ?

Sylwia: A rysując ten wykres czym mam sie sugerować oprócz tych wyliczeń liczyć dla jakiego x ile równa się y podstawiając do f(x) jestem zagubiona

Sylwia: no i czy te granice właściwie liczę ?

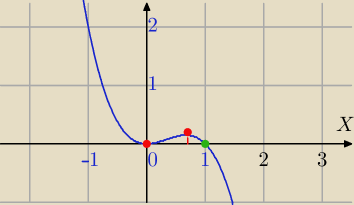Mila: f(x)=x²−x³ 1) D=R brak asymptot pionowych 2) Miejsca zerowe: x²−x³=0⇔ x²*(1−x)=0 x=0 lub x=1 3) granice na krańcach dziedziny: lim_x→∞[x²*(1−x)]=∞ lim_x→∞[x²*(1−x)]=−∞ Brak asymptot poziomych i ukośnych 4) Ekstrema i monotoniczność. f'(x)=(x²−x³)'=2x−3x² f'(x)=0⇔2x−3x²=0⇔x*(2−3x)=0

	2
x=0 lub x=
	3

	2
f'(x)>0⇔x*(2−3x)>0⇔x∊(0,		) ⇔
	3

	2
f(x) jest rosnąca w przedziale (0,		)
	3

f(x) malejąca dla x<0

	2
f(x) malejąca dla x>
	3

Dla x=0 funkcja ma minimum f(0)=0 ( pochodna zmienia znak przy przejściu przez zero z ujemnej na dodatnią)

	2
dla x=		ma maksimum lokalne
	3

	2		4		8		4
f(		)=		−		=
	3		9		27		27

5) Zw_f=(−∞,∞) Szkicujesz wykres: ♦zaznaczasz miejsca zerowe , ekstrema ♦Zaczynasz z lewej strony, funkcja malejąca aż do osiągnięcia wartości zera,

	4
potem rośnie do wartości		, i ponownie maleje przechodząc przez punkt (1,0).
	27

♦Możesz obliczyć jakieś dwie wartości z lewej strony OY i dla x>1, poprawić wykres. ♦Jeszcze raz sprawdzić .

Sylwia: no to mi ulżyło ... dziękuję Mila − jednak coś tak kumam Twój opis jest bardziej czytelny a co z wypukłością ? f(x) jest wypukła gdy f '' >0 u nas f " = 2−6x czyli f " > ¹₃ ? f(x) jest wklęsła gdy f '' <0 u nas f " = 2−6x czyli f " < ¹₃?

J: odwrotnie

Sylwia: a tak bo dzielimy przez minus − dziękuję