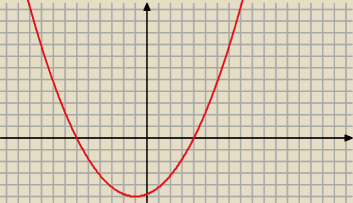
funkcja kwadratowa kropka.: Funkcja kwadratowa f ma dwa miejsca zerowe 4 i −6, a jej najmniejsza wartość jest równa −5. a) napisz wzór tej funkcji w postaci ogolnej. b) wyznacz zbiór tych argumentów, dla których funkcja f przyjmuje wartości większe od 120. Wiem że: x1= 4 x2= −6 q= −5 p= −1 I co dalej? Mam chyba jakieś zaćmienie umysłu Pomoże ktoś?

Janek191: Inny sposób:

	x1 + x2
p =		= − 1
	2

q = − 5 więc f(x) = a*( x − p)² + q = a*( x + 1)² − 5 oraz f(4) = 0 czyli a*5² − 5 = 0 ⇒ 25 a = 5 ⇒a = 0,2 y = 0,2*( x + 1)² − 5 lub y = 0,2*( x² + 2 x + 1) − 5 = 0,2 x² + 0,4 x + 0,2 − 5 y = 0,2 x² + 0,4 x − 4,8 − postać ogólna ================== y > 120 ⇔ 0,2 x² + 0,4 x − 4,8 > 120 2 x² + 4 x − 48 − 1200 > 0 x² + 2 x − 624 > 0 Δ= 4 − 4*1*(−624) = 4 + 2 496 = 2 500 √Δ = 50

	− 2 − 50		− 2 + 50
x =		= − 26 lub x =		= 24
	2		2

więc x ∊ ( −∞; − 26) ∪ ( 24; +∞) ====================