Wyznacz dziedzinę funkcji, ekstrema lokalne oraz przedziały monotoniczności Ewa: Witam, mam problem z dwoma przykładami:

	−x2
a) f(x)= e		,x∊R
	2

	−x2
e jest podstawą ,		jest potęgą
	2

b) f(a)=ln(1+a²)

Janek191: a) f(x) = e^−0,5x2 Df = ℛ

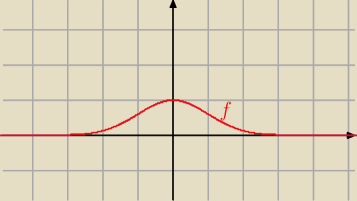
Janek191: f '(x) = e^{−0,5 x2}*( −0,5 x²) ' = −x*e^{−0,5 x2} ⇔ 0 ⇔ x = 0 Dla x < 0 jest f '(x) > 0, a dla x > 0 f '(x) < 0 zatem funkcja f osiąga maksimum w punkcie x = 0 f rośnie w ( − ∞ , 0), bo f '(x) > 0 f maleje w ( 0 ; +∞), bo f '(x) < 0

Ewa: ok. Nawet rozumiem

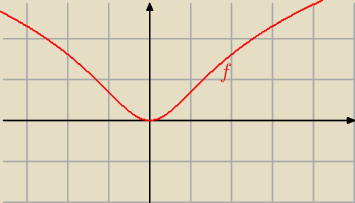
Janek191: f(x) = ln ( 1 + x²) Df = ℛ

	1		1		2x
f '(x) =		*( 1 + x2) ' = 2 x*		=		= 0 ⇔ x = 0
	1 + x2		1 + x2		1 + x2

Dla x < 0 jest f '(x) < 0 , a dla x > 0 jest f '(x) > 0 ; 1 + x² > x dla x∊ℛ więc f osiąga w zerze minimum . Funkcja f maleje w ( −∞; 0) , a rośnie w ( 0; +∞). Patrz też na wykres

Janek191: Tam miało być: 1 + x² > 0 dla x ∊ℛ

Ewa: dziękuję bardzo