przebieg zmienności funkcji wiki999999: Zbadaj przebieg zmienności funkcji f(x)= (x²−3x)/x²−4 policzyłem dziedzine D∊R bez 2 i −2 ponadto policzyłem pochodną od funkcji i po przekształceniach otrzymałem 3x²−8x+12 / (x²−4)² i nie wiem co dalej pomocy

Janek191:

	( 2 x − 3)*(x2 − 4) − ( x2 − 3 x)*2x
f '(x) =		=
	(x2 − 4)2

	2 x3 − 8 x − 3 x2 + 12 − 2 x3 +6 x2
=		=
	(x2 − 4)2

	3 x2 − 8 x + 12
=
	(x2 − 4)2

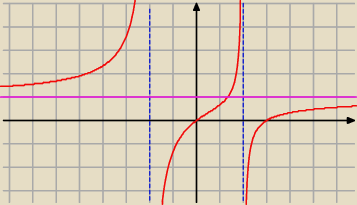
f '(0) = 0 ⇔ 3 x² − 8 x + 12 = 0 Δ = 64 −4*3*12 < 0 więc 3 x² − 8 x + 12 > 0 dla x ≠ − 2 i x ≠ 2 Funkcja f rośnie w : ( −∞ ; − 2), ( − 2, 2),( 2; + ∞) lim f(x) = 1 x→∞ oraz lim f(x) = 1 x → −∞ Asymptota pozioma: y = 1 Asymptoty pionowe: x = − 2 i x = 2

wiki999999: dziękuje kurcze zapomniałem zeby f'(X) przyrownac do zera....juz nie mysle dzisiaj−,− dziekuje jeszcze raz

5-latek: Brakuje określenia czy ta funkcja jest parzysta czy nieparzysta . Także czy funkcja jest okresowa

Janek191: Tam powinno być: f '(x) = 0 ⇔ 3 x² − 8 x + 12 = 0 Granice jednostronne w − 2 i w 2 umiesz policzyć ?

wiki999999: w sensie dla −2 i 2 z prawej i z lewej strony ? chyba umiem xD

Janek191: Tak. To policz lim f(x) x→ 2⁺

wiki999999: no wychodzi dla 2 z prawej −∞ a dla 2 z lewej∞ tak ?

wiki999999: czyli istnieje asymptota pionowa

Janek191: Tak.