Geometria - sprawdzenie kilku zadań Gravity: Mam prośbę. Dostałem do rozwiązania taką kartkę z zadaniami http://zapodaj.net/adf25eace2985.jpg.html rozwiązałem zadania ale nie mam wyników a wolałbym żeby wszystko było ok. Jeśli gdzieś jest błąd to wskazcie mi go i podajcie proszę poprawny wynik jak komuś się chce razem ze sposobem rozwiązania http://zapodaj.net/5c9afd25544f9.jpg.html http://zapodaj.net/da2f59e9e52d7.jpg.html

Mila: Przecież nie wiadomo o jakie bryły chodzi.

Gravity: ? Dałem 3 zdj. Na pierwszym są polecenia a na drugim i trzecim rozwiązania oznaczone których zadań dotyczącą

Mila: 3) dobrze. 4) dobrze. 5) chyba: P_c= 216+2*54√3

Gravity: Dziękuję w piątym rzeczywiście zapomniałem. Pomożesz też z 1 i 2?

Mila: 1) Dobrze, drugie liczę.

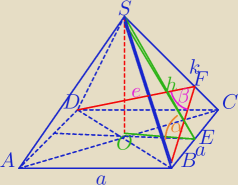
Mila: Pole powierzchni bocznej ostrosłupa prawidłowego czworokątnego jest dwa razy większe od pola podstawy. Oblicz kosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy oraz kosinus kąta między ścianami.

	1
Pb=4*		*a*h
	2

P_ABCD=a²

	1
4*		*a*h=a2⇔
	2

h=a W ΔSOE:

	|OE|		12a		1
cosα=		=		=
	h		a		2

WΔSEC:

	1
k2=a2+(		a)2
	2

	5
k2=		a2
	4

	a√5
k=
	2

	1		1
PΔBCS=		a*a=		a2
	2		2

	1
PΔBCS=		*k*e⇔
	2

1		a√5		1
	*		*e=		a2
2		2		2

	2√5a
e=
	5

Z tw. cosinusów w ΔDBF: (a√2)²=e²+e²−2*e*e*cosβ 2a²=2e²*(1−cosβ)⇔a²=e²*(1−cosβ)

	4a2		4
a2=		*(1−cosβ)⇔1=		*(1−cosβ)
	5		5

	1
cosβ=−
	4

==============

Gravity: Bardzo dziękuję