Funkcja Mufasa: Funkcja f(x) = mx + m² jest malejąca, a jej wykres przechodzi przez punkt (1, 2). Wyznacz m oraz oblicz pole trójkąta ograniczonego wykresem funkcji i osiami układu współrzędnych. Jak wyznaczyć m?

J: prosto: 2 = m + m² i m < 0

Janek191: m < 0 A = (1, 2) więc f(1) = 2 ⇔ m*1 + m² = 2 ⇔ m² + m − 2 = 0 ⇔ ( m +2)*(m − 1) = 0 m = − 2 lub m = 1 − odpada m = − 2 =====

Mufasa: Dobra to teraz jak mam znaleźć ten trójkąt?

J: narusuj sobie tą prostą i odczytaj długość podstawy i wysokości

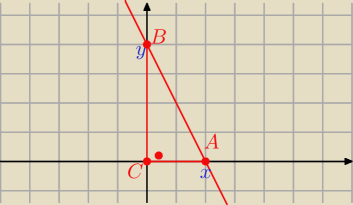
Janek191: f(x) = − 2 x + 4 Znajdź punkty przecięcia prostej o równaniu y = − 2x + 4 z osiami, a następnie oblicz pole Δ prostokątnego .

Mufasa: No właśnie problem w tym, że nie wiem jak ta prosta będzie biec. Jak to wyznaczyć?

Mufasa: Dobra, teraz już wiem.

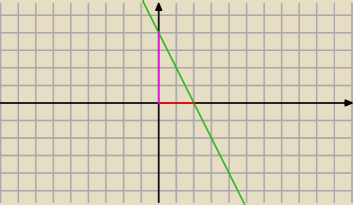
Tadeusz: a jak chcesz "się zabawić" to wykorzystaj równanie prostej w postaci odcinkowej Twoja prosta w postaci kierunkowej to y=−2x+4

	x		y
2x+y=4 ⇒		+		=1 i wszystko jasne
	2		4

Mufasa: Dzięki Tadek, ale wystarczyło policzyć jeden dodatkowy punkt i już wiem jak biegnie ta prosta. Tak jak na twoim rysunku wyszedł mi trójkąt 4, 2, c (2√5). Policzyć jego pole to już dla mnie nie problem. Dziękuje.

Tadeusz: a tak między nami to: −to c nie jest Ci potrzebne ... choć policzyłeś je źle −postać odcinkowa równania prostej jest zapomniana dlatego chciałem ją "wtrącić"

Mufasa: No to dla pewności. Skoro a = 4, b = 2, c = ? − trójkąt prostokątny. To: a² + b² = c² −−−> 4² + 2² = c² −−−> c² = 16 + 4 = 20 −−> c = √20 = 2{p5}

	1		1
No i teraz można liczyć		a(c)*h lub		a(a)*h(b)
	2		2

Policzyłem drugim sposobem, pole trójkąta wynosi 4. Jeśli się mylę wyprowadźcie mnie z błędu.

J:

	1
ale kombinujesz ... P =		2*4 ( patrz na rysunek)
	2