Nikka:
Spróbuję

| | 2P | |
Promień okręgu wpisanego w trójkąt wyraża się wzorem r = |
| gdzie P−pole trójkąta; |
| | a+b+c | |
a,b,c − długości boków trójkąta.
| | 1 | |
P = |
| a*b bo trójkąt prostokątny |
| | 2 | |
Ze wzoru na r ( i r=1) pole jest równe:
ab = a+b+c → c = ab − (a+b)
Z tw. Pitagorasa c
2 = a
2 + b
2
[ab−(a+b)]
2 = a
2 + b
2
a
2b
2 − 2ab(a+b) + (a+b)
2 = a
2 + b
2
a
2b
2 − 2a
2b − 2ab
2 + a
2 + 2ab + b
2 = a
2 + b
2
a
2b
2 − 2a
2b − 2ab
2 + 2ab = 0
ab(ab − 2a − 2b +2) = 0
ab≠0 bo a, b − długości boków trójkąta czyli
ab − 2a − 2b +2 = 0
a(b−2) − 2b + 4 − 2 = 0 (dodaję i odejmuję po lewej stronie 2)
a(b−2) −2(b−2) = 2
(b−2)(a−2) = 2
Z powyższego iloczyn dwóch liczb ma być równy 2, czyli możemy rozpatrzyć dwa iloczyny
1*2 lub 2*1
Z pierwszego iloczynu:
b−2 = 1 i a−2 = 2 → b = 3 i a = 4 i z tw. Pitagorasa c = 5
Z drugiego:
b−2 = 2 i a−2 = 1 → b = 4 i a = 3 i c = 5.
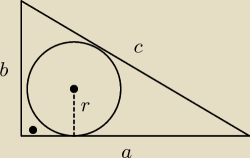
 Pomóżcie Promień okręgu wpisanego w trójkąt prostokątny ma długość 1 . Obliczyć
długości boków tego trójkąta wiedząc, że są one liczbami całkowitymi.
Pomóżcie Promień okręgu wpisanego w trójkąt prostokątny ma długość 1 . Obliczyć
długości boków tego trójkąta wiedząc, że są one liczbami całkowitymi.
 Spróbuję
Spróbuję 


 mam nadzieję, że nic nie namieszałam
mam nadzieję, że nic nie namieszałam 