z
kevs: Kiedy wartość maksymalna wierzchołka f. kwadratowej jest minimalna ? Chodzi o zadanie z
parametrem.
Jakie będą założenia ?
22 lis 20:06
J:
podaj treść zadania
22 lis 20:08
kevs: Wyznacz takie m, aby największa wartość f(x)=−x2+mx+m była najmniejsza z możliwych.
22 lis 20:09
J:
| | Δ | | m2 + 4m | |
yw = − |
| = |
| .. |
| | −4 | | 4 | |
i ustal jaka jest najmniejsza warość tego wyrażenieności od m
22 lis 20:14
kevs: | | −Δ | | 1 | |
Wyznaczam sobie q= |
| = |
| m2+m tylko kiedy to będzie najmniejsze ? |
| | 4a | | 4 | |
22 lis 20:15
J:
wtedy, gdy: m2 + 4m = 0
22 lis 20:16
J:
popraw zapis z 20:15
22 lis 20:16
kevs: co jest nie tak w tym zapisie ?
22 lis 20:17
J:
sorry ... wtedy,gdy: m2 + 4m osiągnie najmniejszą wartość
22 lis 20:17
kevs: No właśnie, ale kiedy osiągnie najmniejszą, bo jakoś tego nie widzę ?
22 lis 20:18
J:
jest OK .. nie zauważyłem,że podzieliłeś/as
22 lis 20:19
kevs: Wyliczyłbym min. wartość z pochodnej zapisując
| | 1 | |
f(m)= |
| m2+m, ale chyba mi nie wyjdzie poprawnie ? |
| | 4 | |
22 lis 20:19
J:
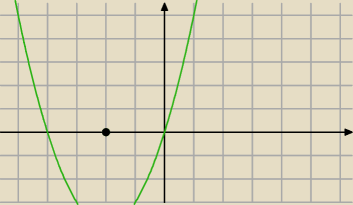
to jest wykres: m
2 + 4m
mimimum dla: m = −2
22 lis 20:20
kevs: aa bo dla tej funkcji faktycznie wyliczyć powinienem p, czyli punkt na osi OX, a nie OY.
Dzięki wielkie.
22 lis 20:22