.
Ola: Mógłby ktoś sprawdzić czy dobrze?
Określ w jakich przedziałach funkcja jest wklęsła/wypukła. Podaj punkty przegięcia
f''(x) = U{−4x
5+16x
3+48x}{{x
2+2)
2}
WK: U{−4x
5+16x
3+48x}{{x
2+2)
2} = 0
x(x
4−4x
2−12)=0 i x
2=t
x=0 lub x=
√6 lub x=−
√6
funkcja wygląda tak: x(x−
√6)
2(x+
√6)
2 (dobrze?)
jesli narysuje teraz wykres, zaczynajac od dołu to
funkcja jest wklęsła w przedziale (0,
√6) suma (
√6,
∞)
wypukła (−
∞,−
√6) suma (−
√6,0)
punkty przegięcia: −
√6,0,
√6
coś jest źle, tylko nie wiem co.
22 lis 19:07
Janek191:
22 lis 19:29
Janek191:
f '(x) = 0 ⇔ x = 0
22 lis 19:33
Janek191:
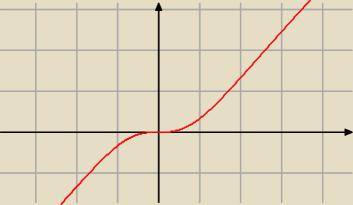
Nie chce mi się liczyć, ale z wykresu wynika,że
x = 0 − punkt przegięcia
W ( − ∞ ; 0 ) funkcja jest wklęsła
W ( 0 ; +∞ ) funkcja jest wypukła.
22 lis 19:37
Ola: ale ma tu jakies znaczenie f'(x)?
myslalem, ze badajac wkleslosc/wypuklosc warunek konieczny stosujemy tylko do f''(x)
zreszą i tak przy f''(x)=0 jednym z rozwiazan jest x=0
nadal nie rozumiem. mógłby ktoś wskazać moje błędy przy rozwiązaniu?
22 lis 19:38
Ola: niestety nie, mogę Ci podać odpowiedzi.
22 lis 19:39
Ola: f. jest wypukla (−∞,−√6) oraz (0,√6)
f. jest wklesla (−√6,0) oraz (√6,∞)
−√6, √6, 0 − punkty przegięcia.
to są odpowiedzi z tyłu ksiązki.
22 lis 19:40
J:
funkcja jest wypukła w tych przedziałach, gdzie druga pochodna jest dodatnia
22 lis 19:41
Ola: wiem, dlatego pytam co jest źle.
rysuję x(x−√6)2(x+√6)2
zaczynając od dołu, odbijając przy −√6 i √6
wychodzi mi tak jak pisałam na początku, co jest źle?
22 lis 19:48
Janek191:
| | x*(x −√6)2*( x +√6)2 | |
f '' ( x) = |
| ; gdzie m > 0 |
| | m | |
więc
dla x < 0 jest f '' (x) < 0, więc funkcja f jest wklęsła
oraz
dla x > 0 jest f ''(x) > 0 , więc funkcja f jest wypukła.
Koniec.
22 lis 19:51
Ola: o to mi chodziło, dziękuję bardzo

22 lis 19:54
Janek191:
Pomyłka, bo również dla x = −√6 i x = √6 są punkty przegięcia.
22 lis 19:56

