rownanie Zadaniematematytetyczne: rozwiaz rownanie x + y −x² −y² = 0

PW: x² − x + y² − y = 0

	1		1		1		1
x2 − x + (		)2 −(		)2 + y2 − y + (		)2 −(		)2 = 0
	2		2		2		2

	1		1		1
(x−		)2 + (y−		)2 = 2(		)2
	2		2		2

Eta:

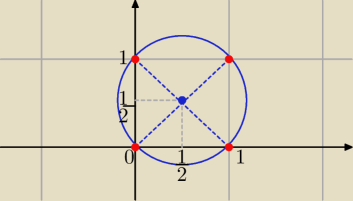
	1		1		1
x2−x+y2−y=0 ⇔o:(x−		)2+(y−		)2=		−−− równanie okręgu
	2		2		2

	1		1		√2
S(		.		) r=
	2		2		2

W liczbach rzeczywistych równanie ma nieskończenie wiele rozwiązań są to pary (x,y) należące do tego okręgu w liczbach całkowitych lub naturalnych równanie ma cztery rozwiązania (0,0) , (0,1), (1,0) , (1,1)