Odległość punktu od prostej jozio: Wyznacz równanie prostej równoległej do prostych k i l oraz równo odległej od każdej z nich. k: 1,4x+2y+10=0 l: 7x+10y−20=0

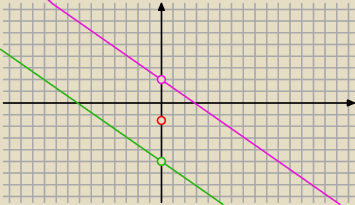
Tadeusz: k: y=−0,7x−5 l: y=−0,7x+2 i chyba wszystko jasne

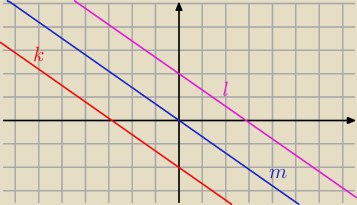
Janek191: k : 1,4 x + 2y + 10 = 0 / * 5 7 x + 10 y + 20 = 0 l : 7 x + 10 y − 20 = 0 m : 7 x + 10 y + p = 0

20 − p		p + 20
	=
√72 + 102		√49 + 100

20 − p = p + 20 p = 0 ==== m : 7 x + 10 y = 0 ===============

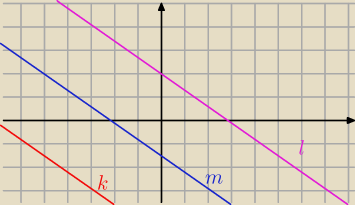
Janek191: Pomyliłem się przy mnożeniu. k : 7 x + 10 y + 50 = 0 l : 7 x + 10 y − 20 = 0 50 − p = 20 +p 2 p = 30 p = 15 ===== m : 7 x + 10 y + 15 = 0 =====================

jozio: a skąd się bierze 3 linijka Twojego rozwiązania?

Janek191: Patrz: 18.31

50 − p		p − (−20)
	=
√72 + 102		√72 + 102

więc 50 − p = p + 20 30 = 2p p = 15 ===== A x + B y + C₁ = 0 A x + B y + C₂ = 0 Odległość tych prostych:

I C1 − C2I
√ A2 + B2

Tadeusz: józio ... ten wzór to konieczność jeśli masz policzyć odległość ... tyle, że nikt Cię o nią nie pyta Piszesz równania prostych w postaci kierunkowej Znasz a ...znasz b_k i b_l Skoro szukana prosta n ma być równoległa do danych prostych to jej b_n=−1,5 a równanie y=−0,7x−1,5 Jeśli potrzebujesz w postaci ogólnej to 0,7x+y+1,5=0 ⇒ lub jak wolisz 7x+10y+15=0

Tadeusz: miało być "równoległa i równoodległa" od danych prostych