Jeden z boków kwadratu opisanego na okręgu o środku w punkcie P jest zawarty...
Olciak: Jeden z boków kwadratu opisanego na okręgu o środku w punkcie P jest zawarty w prostej w
prostej k. Wyznacz równania prostych zawierających pozostałe boki tego kwadratu. P(3,1), k:
y=−34x+10 Wychodzą mi tak kosmiczne liczby, że proszę o rozwiązanie jak najkrótszym sposobem,
ja robiłam przez wyznaczanie środków, obliczenie boku kwadratu (najpierw r, czyli 1/2a), ale
nic mi nie wychodzi
20 lis 23:02
5-latek: Pokaz co wychodzi
20 lis 23:04
Olciak: r=175
czyli a=1045
srodek boku lezaego n prostej k to (61625,5825
20 lis 23:06
Olciak: wierzcholki na k to:
(0,10), a drugi to(12,48;0,64)
a dwa kolejne nie wychodzą

20 lis 23:07
Mila:
Może równanie ma postać:
20 lis 23:31
Olciak: tak, w tresci źle napisałam
20 lis 23:35
Olciak: up
20 lis 23:43
Mila:
Oj, nacisnęłam jakiś klawisz i wszystko zgubiłam, jutro napiszę. Wyniki nieładne.
Dobranoc

21 lis 00:15
5-latek: Milu 
Zanim pojdziesz spac możesz spojrzeć na moje wypociny?
21 lis 00:21
Mila:
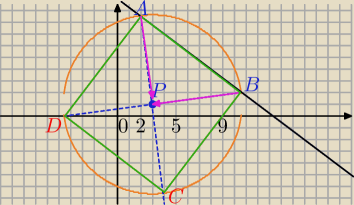
P(3,1),
k: 3x+4y−40=0
r jest równe odległości punktu P od prostej k.
| | 3*3+4*1−40| | |
r=d(P,k)= |
| |
| | √32+42 | |
| | 27 | |
r= |
| − promień okręgu wpisanego w kwadrat. |
| | 5 | |
| | 27√2 | |
R=r*√2= |
| − promień okręgu opisanego na tym kwadracie |
| | 5 | |
| | 1458 | |
(x−3)2+(y−1)2= |
| równanie okręgu opisanego na kwadracie |
| | 25 | |
Punkty przecięcia z prostą k to dwa szukane wierzchołki , niech to będą A i B.
| | 3 | | 1458 | |
(x−3)2+(− |
| x+9)2= |
| ⇔ |
| | 4 | | 25 | |
Aby nie rozwiązywać równań , wykorzystamy translację punkt P o wektor BP
→ i AP
→
| | 14 | | 2 | |
BP→=[3−10 |
| ,1−2 |
| )] |
| | 25 | | 25 | |
| | 14 | | 2 | | 14 | | 2 | |
P=(3,1)→TBP→⇒D=(3+3−10 |
| ,1+1−2 |
| )=(−4 |
| ,− |
| ) |
| | 25 | | 25 | | 25 | | 25 | |
Wsp. C oblicz podobnie.
21 lis 16:26
Eta:
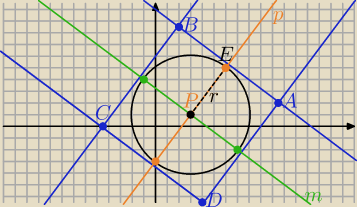
Podaję inny sposób rozwiązania

bez wyznaczania współrzędnych wierzchołków kwadratu
prosta
k =AB: 3x+4y−40=0 P(3,1), r=|PE|
| | |3*3+4*1−40| | | 27 | |
r=d= |
| = |
| |
| | 5 | | 5 | |
prosta CD ∥AB ∥ m to odległość między prostymi CD i m jest równa r
m: 3x+4y+C
1=0 ⇒ 3*3+4*1+C
1=0 ⇒ C
1= −13
| | |C2−13| | |
DC: 3x+4y+C2=0 r= d= |
| −− odległość między prostymi |
| | 5 | |
|C
2−13|=27 ⇒ C
2= −40 lub C
2=14
prosta :
DC: 3x+4y+14=0
prosta AD⊥AB⊥p ⇒ p: 4x−3y+C
3=0 ⇒ 4*3−3*1+C
3=0 ⇒ C
3= −9
| | |C4+9| | |
p: 4x−3y−9=0 to AD: 4x−3y+C4=0 i r=d= |
| −− odległość między prostymi |
| | 5 | |
|C
4+9|=27 ⇒ C
4=18 lub C
4= −36
to
AD: 4x−3y+18=0 i prosta
BC: 4x−3y −36=0
21 lis 22:27
Mila:

21 lis 23:00
Eta:

21 lis 23:03
Mila:
Ja cały czas myślałam, że chodzi o wyznaczenie wsp. wierzchołków
tego kwadratu ( tak dokładnie czytałam! ), ale to też lepiej z odległości prostych
równoległych.
21 lis 23:03
Eta:
Szkoda tylko,że zainteresowanej brak

21 lis 23:04
Mila:
Ostatnio, ciągle tak jest.
Gdzie podziały tamte dziewczyny, gdzie są chłopcy z tamtych lat?
21 lis 23:06
5-latek: Dziewczyny z tamtych lat ?
Za chłopcami poszly w swiat

21 lis 23:10
Eta:
Niedługo zostanie nam tylko "małolatek"

A w środę próbna i..................... będzie

21 lis 23:14
Eta:
O ooo ..... o wilku mowa


21 lis 23:14


 Zanim pojdziesz spac możesz spojrzeć na moje wypociny?
Zanim pojdziesz spac możesz spojrzeć na moje wypociny?
 P(3,1),
P(3,1),
 Podaję inny sposób rozwiązania
Podaję inny sposób rozwiązania  bez wyznaczania współrzędnych wierzchołków kwadratu
prosta k =AB: 3x+4y−40=0 P(3,1), r=|PE|
bez wyznaczania współrzędnych wierzchołków kwadratu
prosta k =AB: 3x+4y−40=0 P(3,1), r=|PE|




 A w środę próbna i..................... będzie
A w środę próbna i..................... będzie 

