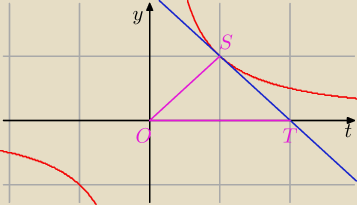
mat kyrtap: Znaleźć równanie krzywej przechodzącej przez punkt (1,1) , dla której pole trójkąta OST (rysunek) utworzonego przez oś Ot, styczną i wektor wodzący punktu styczności jest stałe i równa się 1. rysunek : http://prntscr.com/951eoa

kyrtap: ktoś wie może jak rozwiązać?

kyrtap: Godzio ?

Janek191:

	1
y =
	t

kyrtap: ale ja to mam rozwiązać za pomocą równań różniczkowych

zombi: Zaraz siadam

kyrtap: ok

zombi: Coś mi nie wychodzi ta krzywa xd tzn policzyłem coś, ale dupa. Próbuje jeszcze raz od początku.

kyrtap: jakoś trzeba wykorzystać te pole trójkąta tutaj czyli pewnie jakoś będzie potrzebna wysokość i podstawa ale ja nie wiem jak za to się zabrać

zombi: Może taka dygresja, jak policzyć pole trójkąta Wektor OS = [t₁, y(t₁)] natomiast wektor OT = [0, y₁] y₁ to wartość y, gdy styczna przecina Ox. Pole to | t₁ y(t₁) |

1
	*| |
2

| 0 y₁ | Wyznacznik 2x2.

zombi: Oczywiście źle napisałem OT = [t_x, 0] t_x − wsp. na osi Ot, dla której styczna przyjmuje wartość 0

kyrtap: hmm myślisz zombi że coś ten wyznacznik da?

zombi: Mi nie wychodziło coś ; (

kyrtap: nie lubię tych zadań geometrycznych sprowadzających się do równań różniczkowych

Godzio: Krzywa jest dana wzorem y = y(t) Styczna ma równanie: f(t) = y'(t₀)(t − t₀) + y₀

	y'(t0) * t0 − y0
Szukamy punktu T: 0 = y'(t0)(t − t0) + y0 ⇒ t =
	y'(t0)

Zapisujemy pole trójkąta (przyjmujemy y₀ = y, t₀ = t, y'(t₀) = y' )

y' * t − y   y *   y'
	= 1 ⇒ y * y' * t − y2 = 2y'
2

Teraz trzeba rozwiązać to równanie z warunkiem początkowym y(1) = 1, na to niestety pomysłu nie

	1
mam, ale krzywa y(t) =		spełnia równanie
	t

zombi: http://www.wolframalpha.com/input/?i=yy%27x-y^2+%3D+2y%27 Dokładnie ten sam wynik mi wychodzi, taki jak Godzio przedstawił. Tylko, że z tego

	1
równania nie wychodzi krzywa		, dlatego napisałem że mi nie pyka
	t

kyrtap: spoko już teraz sobie chyba poradzę bo to równanie Bernulliego

kyrtap: Bernoulliego *

Godzio: Może nie wychodzi, ale spełnia

	1		1		1		−2
L = y * y' * t − y2 =		* (−		) * t −		=
	t		t2		t2		t2

	1
P = 2y' = 2 * (−		) = L
	t2

kyrtap: Godzio jak to równanie rozwiązywałeś: y*y'*t − y² = 2y' myślałem że to zwykłe równanie Bernoulliego jednak nie wiem jak tu wyznać rozwiązanie ogólne

kyrtap: wyznaczyć *

kyrtap: lub ty zombi

zombi: Przekształć do postaci

	dy
−y2 + (yt−2)		= 0.
	dt

Trochę przypomina to

	dy
P(x,y) + Q(x,y)		= 0
	dx

Nie sądzisz? Dalej sam próbuj.

zombi: Chyba, że nie miałeś równania różniczkowego zupełnego.

kyrtap: nom tego nie miałem ale się nauczę w takim razie

kyrtap: trochę to przypomina szukanie czy pole jest potencjalne przy analizie wektorowej

J:

	dP(t,y)		dQ(y,t)
zupełne .. nie bardzo ...		= −2y i		= y
	dy		dt

zombi: No tak zupełne nie jest, dlatego trzeba sprawić, zeby takie się stało

Mariusz:

	dy
−y2+(yt−2)		=0
	dt

	dt
−y2		+yt−2=0
	dy

dt		1		2
	−		t+		=0
dy		y		y2

dt		1		2
	−		t=−
dy		y		y2

Równanie liniowe niejednorodne pierwszego rzędu

kyrtap: dzięki za pomoc, chociaż już zdałem egzamin

Mariusz: Widziałem że się chwaliłeś ale chciałem pokazać potomnym że wcale nie trzeba sprowadzać do zupełnego zwłaszcza gdy nie było ono jeszcze wprowadzone (co miało miejsce w twoim przypadku)

kyrtap: tak to prawda już zapisałem to w swoich notatkach, dzięki jeszcze raz