wartość bezwzględna, wykres funkcji
Fed: Hej,
w sumie jest to wycinek z zadania, które mam zrobić, ale jak mam narysować wykres na podstawie
takiego równania?
y = x2 − |x| + 2
20 lis 20:15
Fed: ps. Głównie sprawia mi problem ta wartość bezwzględna, bo gdyby nie ona to jest zwykła funkcja
kwadratowa. Gdzie i dlaczego ta funkcja się odbije?
20 lis 20:17
Mila:
|x|=x dla x≥0
|x|=−x dla x<0
1) x≥0 to f(x)=x
2−x+2 rysujesz parabolę tylko dla x≥0
2)x<0 to f(x)=x
2+x+2 i rysujesz parabolę dla x<0
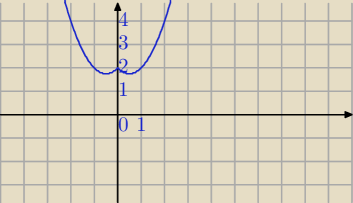
"Zlepek" tych wykresów wygląda tak.
Wniosek sam wyciągnij.
20 lis 22:41
5-latek: Dobry wieczor
Milu 
Fed
Zauwaz z efunkcja f(x)= x
2−|x|+2 jest parzysta bo
f(−x)= (−x)
2−|−x|+2= x
2−|x|+2 czyli f(−x)=f(x)
wiec rusujesz wykres dla x≥0 i odbijasz względem której osi ?
Jeśli nie wiesz to poczytaj
20 lis 22:52
Fed: Dzięki

A jak mam policzyć miejsca zerowe, to po prostu x
2 = x ∪ x
2 = −x, tak? (z definicji o wart.
bezwzgl.)
Bardziej to dotyczy innego, ale podobnego przykładu, i wynik ładny wyszedł, ale się upewniam

20 lis 23:30
PW: Każdemu dodatniemu miejscu zerowemu odpowiada ujemne miejsce zerowe (o tej samej wartości
bezwzględnej). Jest to oczywiste dla każdej funkcji parzystej. Wystarczy więc znaleźć miejsca
zerowe funkcji kwadratowej określonej na dodatniej półosi. Jednak nie w tym zadaniu, badana
funkcja nie ma miejsc zerowych.
20 lis 23:45
Fed: W innym zadaniu nie mam przesunięcia o [0,2], wykres normalnie przecina oś X.
Dzięki.
21 lis 00:43
 |x|=x dla x≥0
|x|=−x dla x<0
1) x≥0 to f(x)=x2−x+2 rysujesz parabolę tylko dla x≥0
2)x<0 to f(x)=x2+x+2 i rysujesz parabolę dla x<0
"Zlepek" tych wykresów wygląda tak.
Wniosek sam wyciągnij.
|x|=x dla x≥0
|x|=−x dla x<0
1) x≥0 to f(x)=x2−x+2 rysujesz parabolę tylko dla x≥0
2)x<0 to f(x)=x2+x+2 i rysujesz parabolę dla x<0
"Zlepek" tych wykresów wygląda tak.
Wniosek sam wyciągnij.
 Fed
Zauwaz z efunkcja f(x)= x2−|x|+2 jest parzysta bo
f(−x)= (−x)2−|−x|+2= x2−|x|+2 czyli f(−x)=f(x)
wiec rusujesz wykres dla x≥0 i odbijasz względem której osi ?
Jeśli nie wiesz to poczytaj
Fed
Zauwaz z efunkcja f(x)= x2−|x|+2 jest parzysta bo
f(−x)= (−x)2−|−x|+2= x2−|x|+2 czyli f(−x)=f(x)
wiec rusujesz wykres dla x≥0 i odbijasz względem której osi ?
Jeśli nie wiesz to poczytaj
 A jak mam policzyć miejsca zerowe, to po prostu x2 = x ∪ x2 = −x, tak? (z definicji o wart.
bezwzgl.)
Bardziej to dotyczy innego, ale podobnego przykładu, i wynik ładny wyszedł, ale się upewniam
A jak mam policzyć miejsca zerowe, to po prostu x2 = x ∪ x2 = −x, tak? (z definicji o wart.
bezwzgl.)
Bardziej to dotyczy innego, ale podobnego przykładu, i wynik ładny wyszedł, ale się upewniam 