Wykres funkcji homograficznej.
miahu: Jak narysować wykres poniższej funkcji?
20 lis 20:11
Janek191:
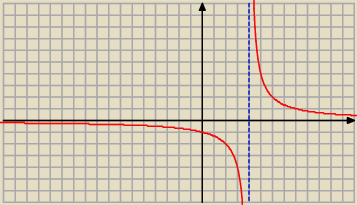
20 lis 20:18
miahu: Okay, dzięki, ale jak dojść do takiego wykresu..?
20 lis 20:20
Janek191:
Policz sobie współrzędne kilku punktów, a następnie połącz je krzywą

| | 4 | | 4 | |
Np. x = − 4 to y = |
| = |
| = − 0,5 |
| | − 4 −4 | | −8 | |
A = ( − 4; −0,5)
| | 4 | | 2 | |
x = − 2 to y = |
| = − |
| |
| | − 2 − 4 | | 3 | |
| | 4 | |
x = 0 to y = |
| = − 1 |
| | 0 −4 | |
C = ( 0 ; − 1)
| | 4 | |
x = 2 to y = |
| = − 2 |
| | 2 − 4 | |
D = ( 2; − 2)
| | 4 | |
x = 3 to y = |
| = − 4 |
| | 3 − 4 | |
E = ( 3; − 4)
itd.
20 lis 20:26
miahu: | | |x| | |
Teraz się zorientowałem, że źle przepisałem wzór funkcji. Chodziło o f(x)= |
| ..  |
| | x−4 | |
20 lis 20:30
Janek191:
Postępujemy tak samo

20 lis 20:33
miahu: Tyle że takiego postępowania nie zaliczą mi na sprawdzianie. Podobno mam zacząć od
zdefiniowania modułu...

20 lis 20:36
PW: Ależ moduł zdefiniowano dawno temu i nie trzeba tego w kółko powtarzać. Na pewnym poziomie
przyjmujemy, że wszyscy wiedzą o co idzie. Przecież w zadaniu z pierwiastkiem nie zaczynasz od
definiowania pierwiastka − wszyscy (?) wiemy co to jest.
Można po prostu narysować wykresy dwóch funkcji:
| | −x | |
f1(x) = |
| , x∊(−∞, 0) |
| | x−4 | |
i
| | x | |
f2(x) = |
| , x∊<0, 4)∪(4,∞), |
| | x−4 | |
które "sklejone" dają wykres funkcji f.
20 lis 22:11




